安徽省淮南市志诚教育十校联盟2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期：2020-11-24 类型：月考试卷
一、单选题
-
1. 下列四个图形中，全等的图形是（ ）
A、①和② B、①和③ C、②和③ D、③和④2. 下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（ ）A、3，3，6 B、1，5，5 C、1，2，3 D、8，3，43. 如图所示，在 中， 平分 ， 于 ， ， ， ，则 长是（ ）
A、4 B、5 C、6 D、74. 已知一个等腰三角形的两边长a、b满足方程组 则此等腰三角形的周长为（ ）A、5 B、4 C、3 D、5或45. 一个多边形的每个内角均为108º，则这个多边形是（ ）A、七边形 B、六边形 C、五边形 D、四边形6.如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1 ， P2 ， P3 ， P4四个点中找出符合条件的点P，则点P有（ ）
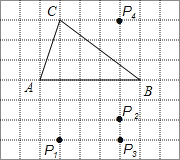A、1个 B、2个 C、3个 D、4个7. 如图，已知AB∥CD ， OA、OC分别平分∠BAC和∠ACD ， OE⊥AC于点E ， 且OE=2，则AB、CD之间的距离为（ ）
A、2 B、4 C、6 D、88. 如图，在△ABC中，已知点D ， E ， F分别为BC ， AD ， AE的中点，且S△ABC＝12cm2 ， 则阴影部分面积S＝（ ）cm2 ．
A、1 B、2 C、3 D、49. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A=（ ）.
A、60° B、80° C、70° D、50°10. 如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，……，照这样走下去，他第一次回到出发地A点时，一共走的路程是（ ）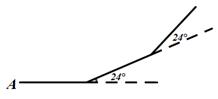
A、140米 B、150米 C、160米 D、240米二、填空题
-
11. 一个三角形的两边长分别是3和8，周长是偶数，那么第三边边长是.12. —个多边形的内角和是其外角和的4倍，则这个多边形的边数是.13. 等腰三角形一腰上的高与另一腰的夹角为20°，则该等腰三角形的底角的度为.14. 如图，在△ABC中，∠B＝46°，三角形的外角∠DAC和∠ACF的平分线交于点E ， 则∠AEC＝ ．
15. 如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分成三个三角形，则 ： ： 等于 ．
16. 如图是某中学某班的班徽设计图案，其形状可以近似看作正五边形，则每一个内角为度；
17. 如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝ .
18. 如图，在△ABC中，AB=8，AC=6，则BC边上的中线AD的取值范围是.
三、解答题
-
19. 某零件如图所示，图纸要求∠A=90°，∠B=32°，∠C=21°，当检验员量得∠BDC=145°，就断定这个零件不合格，你能说出其中的道理吗？
20. 如图，线段AB、CD相交于点O，AD、CB的延长线交于点E，OA=OC，EA=EC，求证：点O在∠AEC平分线上.
21. 在△ABC中，D是AB的中点，E是CD的中点．过点C作CF∥AB交AE的延长线于点F，连接BF．求证：DB=CF．
