安徽省合肥市蜀山区五十中新校2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期:2020-11-24 类型:月考试卷
一、单选题
-
1. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 平面直角坐标系中,线段CD是由线段AB平移得到的,点A(-1,4)的对应点C(4,7),点B(-4,-1)的对应点D的坐标为( )A、(-1,-4) B、(1,-4) C、(1,2) D、(-1,2)3. 一个正比例函数的图象经过点 ,它的表达式为( )A、 B、 C、 D、4. 李老师骑自行车上班,最初以某一速度行进,中途由于自行车发生故障,停下来修车耽误了8分钟,为了按时到校,李老师加快了速度,但仍保持匀速,结果准时到校.下面四个示意图可表示李老师上班过程中自行车行驶路程ym)与行驶时间x小时)的函数关系的是( )A、
 B、
B、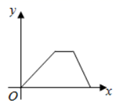 C、
C、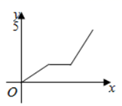 D、
D、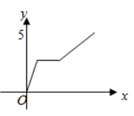 5. 如图,已知表示棋子“馬”和“車”的点的坐标分别为(4,3)、(﹣2,1),则表示棋子“炮”的点的坐标为( )
5. 如图,已知表示棋子“馬”和“車”的点的坐标分别为(4,3)、(﹣2,1),则表示棋子“炮”的点的坐标为( ) A、(1,3) B、(﹣3,3) C、(0,3) D、(3,2)6. 已知 是关于x的正比例函数,则m的值为( )A、2 B、1 C、0或2 D、07. 一次函数 不经过第三象限,则下列正确的是( )A、k<0,b>0 B、k<0,b≥0 C、k<0,b<0 D、k<0,b≤08. 关于函数 ,下列结论正确的是( )A、图象必经过点(﹣2,1) B、图象经过第一、二、三象限 C、图象与直线 =-2 +3平行 D、 随 的增大而增大9. 无论m为何实数,直线 与 的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 两条直线y=ax+b与y=bx+a在同一直角坐标系中的图象位置可能是( )
A、(1,3) B、(﹣3,3) C、(0,3) D、(3,2)6. 已知 是关于x的正比例函数,则m的值为( )A、2 B、1 C、0或2 D、07. 一次函数 不经过第三象限,则下列正确的是( )A、k<0,b>0 B、k<0,b≥0 C、k<0,b<0 D、k<0,b≤08. 关于函数 ,下列结论正确的是( )A、图象必经过点(﹣2,1) B、图象经过第一、二、三象限 C、图象与直线 =-2 +3平行 D、 随 的增大而增大9. 无论m为何实数,直线 与 的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 两条直线y=ax+b与y=bx+a在同一直角坐标系中的图象位置可能是( )
A、 B、
B、 C、
C、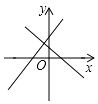 D、
D、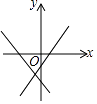
二、填空题
-
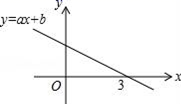
11. 函数 的自变量x取值范围是12. 直线 不经过的象限为 .13. 函数 ,则当函数自变量 时,y=14. 点P先向左平移4个单位,再向上平移1个单位,得到点Q(2,-3),则点P坐标为15. 若函数y=ax+b(a<0)的图象如图所示,则不等式ax+b≥0的解集是 .
 16. 如图,经过点B(-2,0)的直线 与直线 相交于点A(-1,-2),则不等式 的解集为 .
16. 如图,经过点B(-2,0)的直线 与直线 相交于点A(-1,-2),则不等式 的解集为 .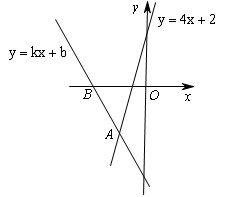
三、解答题
-
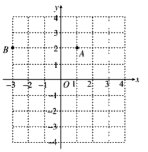
17. 若点( , )在第二象限内,求m的取值范围18. 已知一次函数的图象经过点(1,2),且与直线 相交于点(2,a),求:(1)、a的值;(2)、一次函数的表达式;19. 在平面直角坐标系中,A、B点的位置如图所示;
 (1)、写出点A、B两点的坐标;(2)、若C(-3,-4)、D(3,-3),请在图示坐标系中标出C、D两点;(3)、求出A、B、C、D四点所形成的四边形面积20. 直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)(1)、求直线AB的表达式;(2)、若x轴上有一点C,与点A、B所形成的三角形面积为2,求点C的坐标;21. 医药研究所试验某种新药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是多少小时?
(1)、写出点A、B两点的坐标;(2)、若C(-3,-4)、D(3,-3),请在图示坐标系中标出C、D两点;(3)、求出A、B、C、D四点所形成的四边形面积20. 直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)(1)、求直线AB的表达式;(2)、若x轴上有一点C,与点A、B所形成的三角形面积为2,求点C的坐标;21. 医药研究所试验某种新药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是多少小时? 22. 甲、乙两地相距 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是 以快车开始行驶计时,设时间为 , 两车之间的距离为 ,图中的折线是 与 的函数关系的部分图象,根据图象解决以下问题:
22. 甲、乙两地相距 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是 以快车开始行驶计时,设时间为 , 两车之间的距离为 ,图中的折线是 与 的函数关系的部分图象,根据图象解决以下问题: (1)、慢车的速度是 ,点 的坐标是;(2)、线段 所表示的 与 之间的函数关系式是;(3)、试在图中补全点 以后的图象.23. 合肥庐州食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
(1)、慢车的速度是 ,点 的坐标是;(2)、线段 所表示的 与 之间的函数关系式是;(3)、试在图中补全点 以后的图象.23. 合肥庐州食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
 (1)、方案一中每个包装盒的价格是元.(2)、方案二中租赁机器的费用是元.生产一个包装盒的费用是元.(3)、请分别求出y1、y2与x的函数关系式.(4)、如果你是决策者,生产10000件这样的产品你认为应该选择哪种方案更省钱?并说明理由.
(1)、方案一中每个包装盒的价格是元.(2)、方案二中租赁机器的费用是元.生产一个包装盒的费用是元.(3)、请分别求出y1、y2与x的函数关系式.(4)、如果你是决策者,生产10000件这样的产品你认为应该选择哪种方案更省钱?并说明理由.