浙江省温州市2020-2021学年八年级上学期数学期中考试试卷（A卷）
试卷更新日期：2020-11-23 类型：期中考试
一、选择题（每题3分，共30分）
-
1. 下列标志中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 若等腰三角形的两边长分别为4和6，则它的周长是（ ）A、14 B、15 C、16 D、14或163. 若x > y，则下列式子中，错误的是（ ）A、x - 3 > y - 3 B、x + 3 > y + 2 C、- 3x >- 3y D、 >4. 对于命题“如果∠1 + ∠2 = 90°，那么∠1≠∠2”，能说明它属于假命题的反例是（ ）A、∠1 = 50°，∠2 = 40° B、∠1 = 50°，∠2 = 50° C、∠1 = ∠2 = 45° D、∠1 = 40°，∠2 = 40°5. 下列说法中，正确的是（ ）A、顶角相等的两个等腰三角形全等 B、腰相等的两个等腰三角形全等 C、有一边及一锐角相等的两个直角三角形全等 D、顶角和底边分别相等的两个等腰三角形全等6. 如图所示，∠A0B = 40°，OC平分∠AOB，直尺与OC垂直，则∠1等于（ ）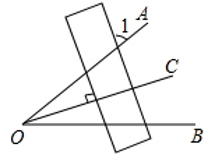
A、60° B、70° C、50° D、40°7. 如图所示，将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起，其中点A′与点A重合，点C′落在边 AB上，连结B′C.若∠ACB = ∠AC′B′ = 90°，AC = BC = 3，则B′C的长为（ ）
A、3 B、6 C、3 D、8. 如图所示，AD是△ABC的角平分线，点O在AD上，且OE⊥BC于点E.若∠BAC = 60°，∠C = 80°，则∠EOD的度数为 （ ）
A、20° B、30° C、10° D、15°9. 如图所示，已知在Rt△ABC中，∠C = 90°，AC = 4，BC = 3，以△ABC的一条边为边画等腰三角形，使它的第三个顶点在△ABC的其他边上，则这样的点有（ ）
A、7个 B、6个 C、5个 D、4个10. 已知△ABC的两条高线AD，BE所在的直线交于点H，若BH = AC，则∠ABC的度数为（ ）A、60° B、45° C、60°或120° D、45°或135°二、填空题（每题4分，共24分）
-
11. 写出一个满足不等式3x + 13≥0的负整数解: （写出一个即可）.12. 如图所示，若FE∥ON，OE平分∠MON，∠FEO = 28°，则∠MFE =.
13. 如图所示，P是∠BAC的平分线上一点，PB⊥AB于点B，且PB = 5 cm，AC = 12 cm，则△APC的面积是 cm2.
14. 在Rt△ABC中，已知直角边长分别是6和8，则斜边上的中线长是 .15. 如图所示，在△ABC中，∠BAC = 110°，EF，MN分别为AB，AC的垂直平分线，如果BC长为不等式3x - 1 < 4x - 5的最小整数解，那么△FAN的周长为 cm，∠FAN = .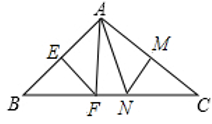
16. 在R△ABC中，∠C = 90°，BC = 8 cm，AC = 6 cm，在射线BC上有一动点D从点B出发，以2 cm/s的速度匀速运动，若点D运动（S）时，以点A，D，B为顶点的三角形恰为等腰三角形，则所用时间t为 s.三、解答题（共66分）
-
17. 解不等式： ，并将其解在数轴上表示出来.18. 如图所示，已知△ABF≌△DEC，说明AC∥DF成立的理由.
19. 已知线段a，b如图所示，请回答下列问题：
(1)、求作：以a，b为边的等腰三角形（要求尺规作图，保留作图痕迹，不写作法）.(2)、若a = 5，b = 6，求（1）中所作等腰三角形的面积.20. 如图所示，在等边三角形ABC的三边上分别取点D，E，F，使AD = BE = CF.
(1)、试说明△DEF是等边三角形.(2)、连结AE，BF，CD，两两相交于点P，Q，R，则△PQR为何种三角形?试说明理由.21. 已知MN⊥PQ，垂足为点O，A，B分别是射线OM，OP上的动点（点A，B不与点O重合）.
(1)、如图1所示，若∠ABO的平分线交∠BAO的平分线于点C，则∠ACB = .(2)、如图2所示，若∠MAB的平分线的反向延长线交∠ABO的平分线于点D，则∠D的度数是 ，并说明理由.(3)、如图3所示，若∠MAB的平分线的反向延长线、∠BAO的平分线分别交∠BON的平分线所在的直线于点E，F.若△AEF中，当有一个角比另一个角大58°时，直接写出∠ABO的度数，为 （不必说明理由）.22. 某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．(1)、求每辆A型车和B型车的售价各为多少元．(2)、甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？23. 已知AE⊥AB，AF⊥AC，AE = AB，AF = AC.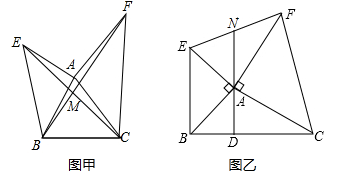
(1)、如图1所示，BF与CE相交于点M.求证：①△ACE ≌△AFB.
②EC⊥BF.
(2)、如图2所示，连结EF，画出△ABC边BC上的高线AD，延长DA交EF于点N，其他条件不变，有下列结论：①∠EAN = ∠ABC；②△AEN ≌△BAD；③S△AEF = S△ABC；④EN = FN.其中正确的结论是 （填序号）.