浙江省宁波市鄞州区2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-11-23 类型:期中考试
一、选择题(本大题共 10小题,每小题 4 分,共 40 分。)
-
1. 若 ,则 的值等于( )A、 B、 C、 D、52. 下列事件中是随机事件的是( )A、通常加热到100℃时,水沸腾 B、在只装有黑球和白球的袋子里,摸出红球 C、购买一张彩票,中奖 D、太阳从东方升起3. 已知⊙O的半径为1cm,点D到圆心O的距离为2cm,则点D与⊙O的位置关系是( )A、点D在⊙O外 B、点D在⊙O上 C、点D在⊙O内 D、不能确定4. 某正方体的平面展开图如图所示,由此可知,原正方体“中”字所在面的对面的汉字是( )
 A、国 B、的 C、中 D、梦5. 如图, DE∥BC ,若 ,则△ADE与四边形BCED的面积的比是( )
A、国 B、的 C、中 D、梦5. 如图, DE∥BC ,若 ,则△ADE与四边形BCED的面积的比是( ) A、1:9 B、1:8 C、1:6 D、1:36. 如图,▱ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A、1:9 B、1:8 C、1:6 D、1:36. 如图,▱ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )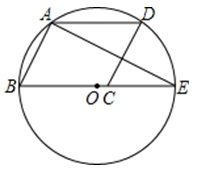 A、36° B、46° C、27° D、63°7. 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
A、36° B、46° C、27° D、63°7. 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( ) A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB上的一个动点,过点P画PD⊥AC于点D,PE⊥BC于点E,当点P由A向B移动时,四边形CDPE周长的变化情况是( )
A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB上的一个动点,过点P画PD⊥AC于点D,PE⊥BC于点E,当点P由A向B移动时,四边形CDPE周长的变化情况是( ) A、逐渐变小 B、逐渐变大 C、先变大后变小 D、不变9. 如图,AC,BC是两个半圆的直径,∠ACP=30°,若AB=2a,则 PQ的值为( )
A、逐渐变小 B、逐渐变大 C、先变大后变小 D、不变9. 如图,AC,BC是两个半圆的直径,∠ACP=30°,若AB=2a,则 PQ的值为( )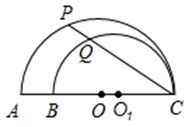 A、a B、1.5a C、 D、10. 如图,四张大小不一的正方形纸片分别放置于矩形的四个角落,其中,①和②纸片既不重叠也无空隙.在矩形ABCD的周长已知的情况下,知道下列哪个正方形的边长,就可以求得阴影部分的周长( )
A、a B、1.5a C、 D、10. 如图,四张大小不一的正方形纸片分别放置于矩形的四个角落,其中,①和②纸片既不重叠也无空隙.在矩形ABCD的周长已知的情况下,知道下列哪个正方形的边长,就可以求得阴影部分的周长( )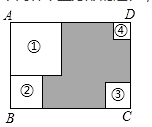 A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题(本大题共6小题,每小题5分,共30分)
-
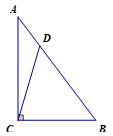
11. 若 , ,则 与 的比例中项为.12. 把抛物线 向左平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为.13. 如图,△ 中, , , ,斜边 上一点 ,使得 ,则 .
 14. 如图,已知AB∥CD∥EF,AD∶AF=3∶5,BE=12,那么CE的长等于.
14. 如图,已知AB∥CD∥EF,AD∶AF=3∶5,BE=12,那么CE的长等于.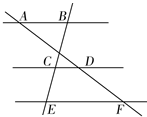 15. 直线 和 在同一直角坐标系中的图象如图所示,则抛物线 的对称轴为
15. 直线 和 在同一直角坐标系中的图象如图所示,则抛物线 的对称轴为 16. 如图,在矩形纸片ABCD中,已知AB=1,BC= ,点E在边CD上移动,连接AE,将多边形ABCE沿AE折叠,得到多边形AB'C'E,点B、C的对应点分别为点B'、C'.当点E从点C移动到点D的过程中,点C'移动的路径长为.
16. 如图,在矩形纸片ABCD中,已知AB=1,BC= ,点E在边CD上移动,连接AE,将多边形ABCE沿AE折叠,得到多边形AB'C'E,点B、C的对应点分别为点B'、C'.当点E从点C移动到点D的过程中,点C'移动的路径长为.
三、解答题(本大题有 8 小题,其中第17——19题各8分;第20——22题各10分;第23题12分,第24题14分,共80分.)
-
17. 计算:(1)、(2)、已知 ,求代数式 的值18. 如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1和图2的正方形网格内按下列要求画出格点三角形.
 (1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .19. 如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀.
(1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .19. 如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀. (1)、从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率.(2)、小明和小亮约定做一个游戏,其规则如下:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表或画树状图的方法说明.(纸牌用A、B、C、D)20. 如图,从观察点A处发现北偏东45°方向,距离为9海里的B处有一走私船。这时一艘缉私艇位于A点的北偏西53°方向的C处,且C点恰好在B点的正西方向。此时走私船正以每小时50海里的速度从B处向北偏东30°方向逃窜,缉私艇奉命立即以每小时50 海里的速度向走私船追去。
(1)、从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率.(2)、小明和小亮约定做一个游戏,其规则如下:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表或画树状图的方法说明.(纸牌用A、B、C、D)20. 如图,从观察点A处发现北偏东45°方向,距离为9海里的B处有一走私船。这时一艘缉私艇位于A点的北偏西53°方向的C处,且C点恰好在B点的正西方向。此时走私船正以每小时50海里的速度从B处向北偏东30°方向逃窜,缉私艇奉命立即以每小时50 海里的速度向走私船追去。 (1)、点B和点C相距多少海里?(2)、缉私艇沿什么方向行驶,才能在最短时间内追上走私船?并求出所需时间.(参考数据:sin53º≈0.8,cos53º≈0.6, )21. 已知二次函数 的图象经过点(1,0)和(0,2).(1)、求b,c的值;(2)、当 时,求 的取值范围;(3)、已经点P(m,n)在该函数的图象上,且 ,求点P的坐标.22. 如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)、点B和点C相距多少海里?(2)、缉私艇沿什么方向行驶,才能在最短时间内追上走私船?并求出所需时间.(参考数据:sin53º≈0.8,cos53º≈0.6, )21. 已知二次函数 的图象经过点(1,0)和(0,2).(1)、求b,c的值;(2)、当 时,求 的取值范围;(3)、已经点P(m,n)在该函数的图象上,且 ,求点P的坐标.22. 如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B. (1)、求证:AD是⊙O的切线;(2)、若BC=8,tanB= , 求⊙O的半径.23. 若抛物线的顶点到 轴的距离与抛物线截 轴所得的距离相等,则称该抛物线是等距抛物线.
(1)、求证:AD是⊙O的切线;(2)、若BC=8,tanB= , 求⊙O的半径.23. 若抛物线的顶点到 轴的距离与抛物线截 轴所得的距离相等,则称该抛物线是等距抛物线. (1)、判断:二次函数 (填“是”或“不是”)等距抛物线;(2)、若抛物线 是等距抛物线,求 的值;(3)、在(2)的条件下,若该抛物线与 轴交于A,B两点(点A在点B的左侧),顶点为C,在此抛物线上是否存在一个点F,使得∠FAB=∠ACB. 若存在,请求出点F的坐标;若不存在,请说明理由.24. 如图1.已知⊙M与x轴交于A、B两点,与y轴交于C、D两点,A、B两点的横坐标分别为﹣1和7,弦AB的弦心距MN为3,
(1)、判断:二次函数 (填“是”或“不是”)等距抛物线;(2)、若抛物线 是等距抛物线,求 的值;(3)、在(2)的条件下,若该抛物线与 轴交于A,B两点(点A在点B的左侧),顶点为C,在此抛物线上是否存在一个点F,使得∠FAB=∠ACB. 若存在,请求出点F的坐标;若不存在,请说明理由.24. 如图1.已知⊙M与x轴交于A、B两点,与y轴交于C、D两点,A、B两点的横坐标分别为﹣1和7,弦AB的弦心距MN为3,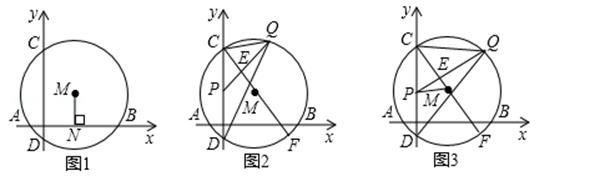 (1)、求⊙M的半径;(2)、求弦CD的长;(3)、如图2,P在弦CD上,且CP=2,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,求CQ的长;(4)、如图3.若P点是弦CD上一动点,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.
(1)、求⊙M的半径;(2)、求弦CD的长;(3)、如图2,P在弦CD上,且CP=2,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,求CQ的长;(4)、如图3.若P点是弦CD上一动点,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.