浙江省杭州市2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-11-23 类型：期中考试

进入出卷网下载

一、仔细选一选（本题有10个小题，每小题3分，共30分）

1. 二次函数 $y = - {(x - 1)}^{2} + 2$ 的最大值是（）

A、-2 B、2 C、-1 D、1

查看试题解析
2. 反比例函数y= $\frac{m + 3}{x}$ ，当x>0时，y随x的增大而增大，那么m的取值范围是( )

A、m<3 B、m>3 C、m<－3 D、m>－3

查看试题解析
3. 在扇形中，∠AOB=90°，面积为4πcm² ，用这个扇形围成一个圆锥的侧面，这个圆锥的底面半径为（）

A、1cm B、2cm C、 $\sqrt{15}$ cm D、4cm

查看试题解析
4. 若将抛物线 $y = 2 x^{2}$ 向右平移3个单位，再向上平移5个单位，得到的抛物线是（）

A、 $y = 2 {(x + 3)}^{2} - 5$ B、 $y = 2 {(x - 3)}^{2} + 5$ C、 $y = 2 {(x - 3)}^{2} - 5$ D、 $y = 2 {(x + 3)}^{2} + 5$

查看试题解析
5. 若点M（x，y）满足 ${(x + y)}^{2} = x^{2} + y^{2} - 2$ ，则点M所在象限是（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、不能确定

查看试题解析
6. 已知x是实数，且满足 $(x - 2) (x - 3) \sqrt{1 - x} = 0$ ，则相应的函数 $y = x^{2} + x + 1$ 的值为（）

A、13 或3 B、7 或3 C、3 D、13或7或3

查看试题解析
7. 如图，⊙O的直径AB=8，P是圆上任一点（A，B除外），∠APB的平分线交⊙O于C，弦EF过AC，BC的中点M、N，则EF的长是（）

A、 $4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、6 D、 $2 \sqrt{5}$

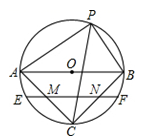查看试题解析
8. 如图，点A是反比例函数y= $\frac{2}{x}$ (x＞0)的图象上任意一点，AB∥x轴交反比例函数y=－ $\frac{3}{x}$ 的图象于点B，以AB为边作▱ABCD，其中C、D在x轴上，则S_▱ABCD为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 在△ABC中，∠ACB为锐角，分别以AB，AC为直径作半圆，过点B，A，C作弧BAC，如图所示.若AB=4，AC=2，图中两个新月形面积分别为S₁ ， S₂ ，两个弓形面积分别为S₃ ， S₄ ， S₁-S₂= $\frac{π}{4}$ ，则S₃-S₄的值是（）

A、 $\frac{29}{4} π$ B、 $\frac{23}{4} π$ C、 $\frac{11}{4} π$ D、 $\frac{5}{4} π$

查看试题解析
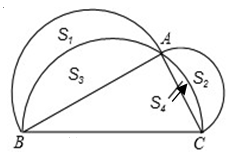10. 关于x的方程 $2 x^{2} + a x + b = 0$ 有两个不相等的实数根，且较小的根为2，则下列结论：
① $2 a + b < 0$ ；② $a b < 0$ ；③关于 $x$ 的方程 $2 x^{2} + a c + b + 2 = 0$ 有两个不相等的实数根；④抛物线 $y = 2 x^{2} + a c + b - 2$ 的顶点在第四象限。
其中正确的结论有（）

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、认真填一填（本题有6个小题，每小题4分，共24分）

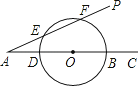
11. 函数 $y = \frac{\sqrt{1 - x}}{x}$ 的自变量x的取值范围是.

查看试题解析
12. 三张完全相同的卡片上分别写有函数y=3x， $y = \frac{3}{x}$ ，y=x² ，从中随机抽取一张，则所得卡片上函数的图象在第一象限内y随x的增大而增大的概率是.

查看试题解析
13.
如图，∠PAC=30°，在射线AC上顺次截取AD=3cm，DB=10cm，以DB为直径作⊙O交射线AP于E、F两点，则线段EF的长是cm．

查看试题解析
14. 如图，已知函数 $y = a x^{2} + b x + c$ 与 $y = - \frac{k}{x}$ 的图象交于A(-4，1)、B(2，-2) 、C(1，-4)三点，根据图象可求得关于x的不等式 $a x^{2} + b x + c < - \frac{k}{x}$ 的解集为.

查看试题解析
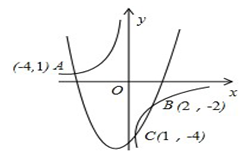15. 如图，在△ABC中，∠ACB=90°，AC=4，BC=3，把△ABC分别绕直线AC，AB旋转一周，所得几何体的表面积分别为S₁ ， S₂ ，则| S₂-S₁|=_（平方单位）.

查看试题解析
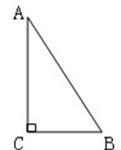16. 如图所示，P₁（x₁ ， y₁）、P₂（x₂ ， y₂），……P_n（x_n ， y_n）在函数y= $\frac{9}{x}$ （x＞0）的图象上，△OP₁A₁ ， △P₂A₁A₂ ， △P₃A₂A₃……△P_nA_n-1A_n都是等腰直角三角形，斜边OA₁ ， A₁A₂……A_n-1A_n ，都在x轴上，则y₁+y₂+…+y_n=.

查看试题解析

三、全面答一答（本题有7个小题，共66分）

17. 已知图中的曲线是函数 $y = \frac{m - 5}{x}$ (m为常数)图象的一支.

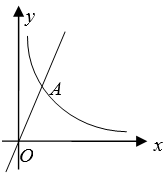(1)、求常数m的取值范围；

(2)、若该函数的图象与正比例函数y=2x图象在第一象限的交点为
A（2，n），求点A的坐标及反比例函数的解析式.

查看试题解析
18.
小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上．

(1)、请你帮小明把花坛的位置画出来（尺规作图，不写作法，保留作图痕迹）．

(2)、在△ABC中，AC=4米，∠ABC=45°，试求小明家圆形花坛的半径长．

查看试题解析
19. 足球比赛中，某运动员将在地面上的足球对着球门踢出，图中的抛物线是足球的飞行高度y（m）关于飞行时间x（s）的函数图象（不考虑空气的阻力），已知足球飞出1s时，足球的飞行高度是2.44m，足球从飞出到落地共用3s.

(1)、求y关于x的函数关系式；

(2)、假设没有拦挡，足球将擦着球门左上角射入球门，球门的高为2.44m（如图所示，足球的大小忽略不计）.如果为了能及时将足球扑出，那么足球被踢出时，离球门左边框12m处的守门员至少要以多大的平均速度到球门的左边框？

查看试题解析
20. 如图，在平的直角坐标系中，直线y=﹣2x+2与x轴y轴分别相交于点A，B，四边形ABCD是正方形，双曲线在第一象限经过点D.

(1)、求双曲线的函数解析式；

(2)、将正方形ABCD沿x轴向左平移多少个单位长度时，点C的对应点恰好落在（1）中的双曲线上，请说明理由.

查看试题解析
21. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴相交于点A，B（点A，B在原点O两侧），与y轴相交于点C，且点A，C在一次函数 $y = \frac{3}{4} x + n$ 的图象上，线段AB长为14，线段OC长为6，当y₁随着x的增大而减小时，求自变量x的取值范围。

查看试题解析
22. 如图1，△ABC内接于半径为4cm的⊙O，AB为直径，弧BC长为 $\frac{4 π}{3} c m$ .

(1)、计算∠ABC的度数；

(2)、将与△ABC全等的△FED如图2摆放，使两个三角形的对应边DF与AC有一部分重叠，△FED的最长边EF恰好经过弧AB的中点M.求证：AF=AB；

查看试题解析
23. 已知抛物线 $y = a x^{2} + b x + c (a > 0)$ 与x轴的两个交点分别为A（－1，0）、B（3，0），与y轴的交点为点D，顶点为C，

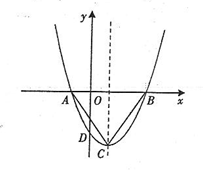(1)、求出该抛物线的对称轴；

(2)、当点C变化，使60°≤∠ACB≤90°时，求出 $\frac{4 \times n π}{180} = \frac{4 π}{3}$ 的取值范围；

(3)、作直线CD交x轴于点E，问：在y轴上是否存在点F，使得△CEF是一个等腰直角三角形？若存在，请求出a的值，若不存在，请说明理由。

查看试题解析