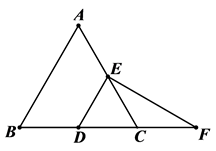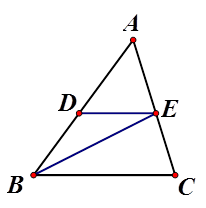浙江省温州市三校2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2020-11-23 类型：期中考试
一、精心选一选（每小题3分，共30分）
-
1. 以下列数据为长度的三条线段，能组成三角形的是（ ）A、1，2，3 B、6, 8, 15 C、8 ,4, 3 D、4, 6, 52. 下列学习用具中，其形状不是轴对称图形的是（ ）A、
B、
C、
D、
3. 如图，△ACB≌△A1CB1 ， AB=2，AC=3，BC=4，则A1 C的长为（ ）
A、2 B、3 C、4 D、2.54. 下列语句是命题的是（ ）．A、等腰三角形是轴对称图形 B、将27开立方 C、画一个角等于已知角 D、垂线段最短吗?5. 若等腰三角形的两边长分别为4和9，则它的周长为（ ）A、13 B、17 C、22 D、17或226. 如果直角三角形的两条直角边的长分别为6cm和8cm，那么斜边上的中线等于（ ）A、2.4cm B、4.8cm C、5cm D、10cm7. 已知AD是△ABC的中线，BE是△ABD的中线，若△ACD的面积为20，则△ABE的面积为（ ）．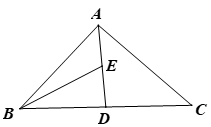
A、5 B、10 C、15 D、188. 下列条件中，不能判断一个三角形是直角三角形的是（ ）A、三条边的比是1∶2∶3 B、三条边满足关系a2=c2－b2 C、三个角的比是1∶2∶3 D、三个角满足关系∠B+∠C=∠A9. 如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于（ ）．
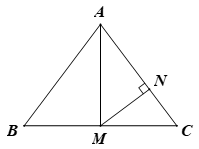A、 B、 C、 D、10. 如图，△ABC的周长为30，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边于点E，连结AD，若AE=4，则△ABD的周长是（ ）
A、22 B、20 C、18 D、15二、细心填一填（本题有8小题，每小题3分，共24分）
-
11. 在△ABC中，∠A:∠B:∠C=1:2:3，则∠A为度.12. 如图，在△ABC中，点D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于.
13. 命题“对顶角相等”改写成“如果…那么…”的形式是 ．14. 如图，在Rt△ABC中，∠C=90°，CD⊥AB，如果∠A=40°，则∠1=度.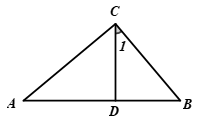
15. 如图，已知AC=DB，再添加一个适当的条件 ， 使△ABC≌△DCB．（只需填写满足要求的一个条件即可）.
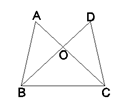16. 如图，△ABC中，AB=AC，BC=3，点E为中线AD上一点，已知△ABE和△CDE的面积分别为1.5和2，则AD的长度为 .
17. 如图，已知△ABD，△BCE均为等腰直角三角形，若CD=8，BE=3，则AC等于 .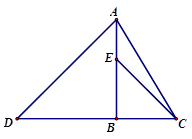
18. 如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成．若较短的直角边BC=2.5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图2所示的“数学风车”，若△BCD的周长是15，则这个风车的外围周长是 ．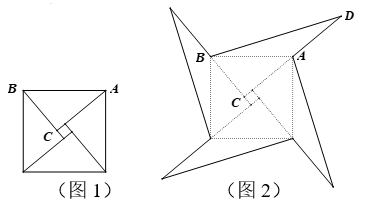
三、动脑想一想（本题有6小题，共46分）
-
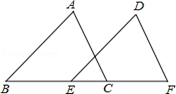
19. 如图，点B、E、C、F在一条直线上，∠B=∠DEF，AB=DE，BE=CF，∠F=70° ， 求∠ACB的度数.
20. 如图，在△ABC 中，AB=AC，D为BC边上中点，DM⊥AC于点M， DN⊥AB 于点N.求证：DM=DN.
21. 已知：如图，A，B，D在同一条直线上，∠1=∠2，∠A=∠D=90°，AC=BD.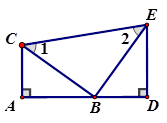
(1)、△ABC与△DEB全等吗？请说明理由；(2)、求证：△CBE为等腰直角三角形.22. 在如图所示的网格中，每个小正方形的边长均为1个单位。
(1)、请你在图1中画一个以格点为顶点，面积为6个平方单位的等腰三角形。(2)、请你在图2中画一条以格点为端点，长度为 的线段.
(3)、请你在图3中画一个以格点为顶点， 为直角边的直角三角形。
