浙江省宁波市慈溪市2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-11-23 类型:期中考试
一、单选题(共10小题,每小题4分,共40分)
-
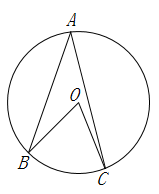
1. 下列函数关系式中,属于二次函数的是( )A、 B、 C、 D、2. 如图,在圆 中,圆心角 ,则圆周角 ( )
 A、 B、 C、 D、3. 下列事件中,属于必然事件的是( )A、三个点确定一个圆 B、每条边都相等的多边形是正多边形 C、平分弦的直径垂直于弦 D、直径所对的圆周角是直角4. 浙江省积极响应国家“节约资源,保护环境”的号召,利用自身地域环境优势,加强可再生资源——风能的利用。其中,海上风电产业具有技术先导性强、经济体量大和产业关联度大的特点。如图是海上风力发电装置,转子叶片图案绕中心旋转 后能与原图案重合,则 可以取( )
A、 B、 C、 D、3. 下列事件中,属于必然事件的是( )A、三个点确定一个圆 B、每条边都相等的多边形是正多边形 C、平分弦的直径垂直于弦 D、直径所对的圆周角是直角4. 浙江省积极响应国家“节约资源,保护环境”的号召,利用自身地域环境优势,加强可再生资源——风能的利用。其中,海上风电产业具有技术先导性强、经济体量大和产业关联度大的特点。如图是海上风力发电装置,转子叶片图案绕中心旋转 后能与原图案重合,则 可以取( ) A、60 B、90 C、120 D、1805. 如图, ,下列比例式中不正确的是( )
A、60 B、90 C、120 D、1805. 如图, ,下列比例式中不正确的是( ) A、 B、 C、 D、6. 如图, ∽ ,且 ,则 与 的相似比为( )
A、 B、 C、 D、6. 如图, ∽ ,且 ,则 与 的相似比为( ) A、2:3 B、3:2 C、2:1 D、1:27. 如图,四边形 内接于圆 ,若 ,则 ( )
A、2:3 B、3:2 C、2:1 D、1:27. 如图,四边形 内接于圆 ,若 ,则 ( ) A、 B、 C、 D、8. 如图, 为半圆的直径,且 . 若将半圆绕点 顺时针旋转 ,使得点 旋转到点 的位置,则图中阴影部分的面积为( )
A、 B、 C、 D、8. 如图, 为半圆的直径,且 . 若将半圆绕点 顺时针旋转 ,使得点 旋转到点 的位置,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 如图是抛物线 的部分图象,其对称轴为直线 ,与 轴的交点坐标为 ,下列结论:① ;② ;③方程 的两根分别是0和2;④方程 有一个实根大于2;⑤当 时, 随着 的增大而减小. 其中正确结论的个数是( )
A、 B、 C、 D、9. 如图是抛物线 的部分图象,其对称轴为直线 ,与 轴的交点坐标为 ,下列结论:① ;② ;③方程 的两根分别是0和2;④方程 有一个实根大于2;⑤当 时, 随着 的增大而减小. 其中正确结论的个数是( )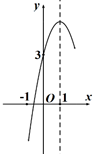 A、2 B、3 C、4 D、510. 如图,扇形 的圆心角的度数为 ,半径长为4, 为弧 上的动点, ,垂足分别为 , 是 的外心.当点 运动的过程中,点 分别在半径上作相应运动,从点 离开点 时起,到点 到达点 时止,点 运动的路径长( )
A、2 B、3 C、4 D、510. 如图,扇形 的圆心角的度数为 ,半径长为4, 为弧 上的动点, ,垂足分别为 , 是 的外心.当点 运动的过程中,点 分别在半径上作相应运动,从点 离开点 时起,到点 到达点 时止,点 运动的路径长( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,每小题5分,共30分)
-
11. 2020年2月,为了支援武汉抗击“新冠肺炎”疫情,某医院从自愿报名的5名男医生和3名女医生中随机挑选一名医生去武汉支援,则选中一名女医生的概率为.12. 已知正 边形的一个内角为 ,则 .13. 在一幅比例尺为1:500000的地图中,小王量出学校到体育馆的距离为2.4厘米,则学校到体育馆的实际距离为千米.14. 将二次函数 的图象先向左平移2个单位,再向下平移4个单位,则所得图象的函数表达式为.15. 高尔夫球运动是一项具有特殊魅力的运动,运动员会利用不同的高尔夫球杆将高尔夫球打进球洞,从而使其在优美的自然环境中锻炼身体,并陶冶情操. 如图,某运动员将一只高尔夫球沿某方向击出时,小球的飞行路线是一条抛物线. 如果不考虑空气阻力等因素,小球的飞行高度 (单位:米)与飞行时间 (单位:秒)之间满足函数关系 .则小球从飞出到落地瞬间所需的时间为秒.
 16. 如图, 是以 为圆心,半径为4的圆的两条弦, ,且点 在 内. 点 是劣弧 上的一个动点,点 分别是 的中点. 则 的长度的最大值为.
16. 如图, 是以 为圆心,半径为4的圆的两条弦, ,且点 在 内. 点 是劣弧 上的一个动点,点 分别是 的中点. 则 的长度的最大值为.
三、解答题(共8大题,第17-19题各8分,第20-22题各10分,第23题12分,第24题14分,共80分)
-
17. 已知抛物线 经过点 .(1)、求 的值及抛物线的顶点坐标;(2)、当 取什么值时, 随着 的增大而减小?18. 已知三条线段 满足 ,且 .(1)、求 的值;(2)、若线段 是线段 和 的比例中项,求 的值.19. 在平面直角坐标系中, 的位置如图所示,其中 , , .
 (1)、画出 绕点 顺时针旋转 后得到的 ;(2)、求旋转过程中动点 所经过的路径长(结果保留 ).20. 为弘扬我校核心文化——“坿”文化,积极培育学生“敢进取”的精神,我校举行一次数学探究实验. 在一个不透明的箱子里放有 个除颜色外其他完全相同的小球(数量不详),只知其中有5个红球.(1)、若先从箱子里拿走 个红球,这时从箱子里随机摸出一个球是红球的事件为“随机事件”,则 的最大值为.(2)、若在原来的箱子里再加入3个红球后进行摸球实验,每次摸球前先将箱子里的球摇匀,任意摸出一个球记下颜色后再放回箱子,通过大量重复摸球实验后发现摸到红球的频率稳定在40%左右,你能估计 的值是多少吗?21. “筒车”是一种以水流作动力,取水灌田的工具。据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造. 明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”的工作原理. 如图,“筒车”盛水筒的运行轨迹是以轴心 为圆心的圆,已知圆心 在水面上方,且当圆被水面截得的弦 为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).
(1)、画出 绕点 顺时针旋转 后得到的 ;(2)、求旋转过程中动点 所经过的路径长(结果保留 ).20. 为弘扬我校核心文化——“坿”文化,积极培育学生“敢进取”的精神,我校举行一次数学探究实验. 在一个不透明的箱子里放有 个除颜色外其他完全相同的小球(数量不详),只知其中有5个红球.(1)、若先从箱子里拿走 个红球,这时从箱子里随机摸出一个球是红球的事件为“随机事件”,则 的最大值为.(2)、若在原来的箱子里再加入3个红球后进行摸球实验,每次摸球前先将箱子里的球摇匀,任意摸出一个球记下颜色后再放回箱子,通过大量重复摸球实验后发现摸到红球的频率稳定在40%左右,你能估计 的值是多少吗?21. “筒车”是一种以水流作动力,取水灌田的工具。据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造. 明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”的工作原理. 如图,“筒车”盛水筒的运行轨迹是以轴心 为圆心的圆,已知圆心 在水面上方,且当圆被水面截得的弦 为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).
 (1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦 从原来的6米变为8米时,则水面上涨的高度为多少米?22. 为贯彻落实全市城乡“清爽行动”暨生活垃圾分类攻坚大会精神,积极创建垃圾分类示范单位,我校举行了一次“垃圾分类”模拟活动. 我们将常见的生活垃圾分为四类:可回收垃圾、厨余垃圾、有害垃圾、其他垃圾,且应分别投放于4种不同颜色的对应垃圾桶中. 若在这次模拟活动中,某位同学将两种不同类型的垃圾先后随意投放于2种不同颜色的垃圾桶.(1)、请用列表或画树状图表示所有可能的结果数;(2)、求这位同学将两种不同类型的垃圾都正确投放的概率.23. “新冠肺炎”疫情期间某工厂为支持国家抗击疫情每天连夜生产急缺的消毒液,已知每瓶消毒液的生产成本为20元,为了合理定价,根据市场调查发现,当销售单价为30元时,每天的销售量为6000瓶,若销售单价每降低1元,则每天能多销售1000瓶,但要求销售单价不能低于成本且不高于30元.(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、求每天的利润 (元)与销售单价 (元)之间的函数关系式;(3)、该工厂负责人决定将每天的利润全部捐献出来进一步支持国家抗击“新冠肺炎”疫情,则当销售单价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图
(1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦 从原来的6米变为8米时,则水面上涨的高度为多少米?22. 为贯彻落实全市城乡“清爽行动”暨生活垃圾分类攻坚大会精神,积极创建垃圾分类示范单位,我校举行了一次“垃圾分类”模拟活动. 我们将常见的生活垃圾分为四类:可回收垃圾、厨余垃圾、有害垃圾、其他垃圾,且应分别投放于4种不同颜色的对应垃圾桶中. 若在这次模拟活动中,某位同学将两种不同类型的垃圾先后随意投放于2种不同颜色的垃圾桶.(1)、请用列表或画树状图表示所有可能的结果数;(2)、求这位同学将两种不同类型的垃圾都正确投放的概率.23. “新冠肺炎”疫情期间某工厂为支持国家抗击疫情每天连夜生产急缺的消毒液,已知每瓶消毒液的生产成本为20元,为了合理定价,根据市场调查发现,当销售单价为30元时,每天的销售量为6000瓶,若销售单价每降低1元,则每天能多销售1000瓶,但要求销售单价不能低于成本且不高于30元.(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、求每天的利润 (元)与销售单价 (元)之间的函数关系式;(3)、该工厂负责人决定将每天的利润全部捐献出来进一步支持国家抗击“新冠肺炎”疫情,则当销售单价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图 (1)、如图①,圆 的半径为2,圆内有一点 , ,若弦 过点 ,则弦 长度的最大值为;最小值为;(2)、如图②,将 放在如图所示的平面直角坐标系中,点 与原点 重合,点 在 轴的正半轴上, , , .在 轴上方是否存在点 ,使得 ,且 ?若存在,请求出点 的坐标;若不存在,请说明理由;(3)、如图③, 是学校的一块空地示意图,其中 , 米, 米.现在学校领导想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建“学生劳动教育基地”.若学校想建的“学生劳动教育基地”是四边形 ,且满足 ,你认为学校领导的想法能实现吗?若能,求出这个四边形“学生劳动教育基地”面积和周长的最大值;若不能,请说明理由.
(1)、如图①,圆 的半径为2,圆内有一点 , ,若弦 过点 ,则弦 长度的最大值为;最小值为;(2)、如图②,将 放在如图所示的平面直角坐标系中,点 与原点 重合,点 在 轴的正半轴上, , , .在 轴上方是否存在点 ,使得 ,且 ?若存在,请求出点 的坐标;若不存在,请说明理由;(3)、如图③, 是学校的一块空地示意图,其中 , 米, 米.现在学校领导想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建“学生劳动教育基地”.若学校想建的“学生劳动教育基地”是四边形 ,且满足 ,你认为学校领导的想法能实现吗?若能,求出这个四边形“学生劳动教育基地”面积和周长的最大值;若不能,请说明理由.