浙江省宁波市慈溪市2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-11-23 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列图案是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 要求画△ABC的边AB上的高,下列画法中,正确的是( )A、
A、1个 B、2个 C、3个 D、4个2. 要求画△ABC的边AB上的高,下列画法中,正确的是( )A、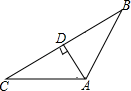 B、
B、 C、
C、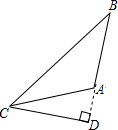 D、
D、 3. 在数学表达式: 中,是一元一次不等式的有 ( )A、1个 B、2个 C、3个 D、4个4. 如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
3. 在数学表达式: 中,是一元一次不等式的有 ( )A、1个 B、2个 C、3个 D、4个4. 如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )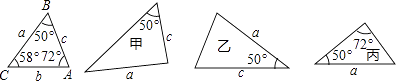 A、甲和乙 B、乙和丙 C、只有乙 D、只有丙5. 已知△ABC的三个边之比为3:4:5,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形6. 下列叙述错误的是( )A、所有的命题都有条件和结论 B、所有的命题都是定理 C、所有的定理都是命题 D、所有的公理都是真命题7. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A、甲和乙 B、乙和丙 C、只有乙 D、只有丙5. 已知△ABC的三个边之比为3:4:5,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形6. 下列叙述错误的是( )A、所有的命题都有条件和结论 B、所有的命题都是定理 C、所有的定理都是命题 D、所有的公理都是真命题7. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( ) A、13 B、26 C、47 D、948. 若关于x的方程 的解是正数,则a的取值范围是( )A、 B、 C、a为任何实数 D、a为大于0的数9. 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
A、13 B、26 C、47 D、948. 若关于x的方程 的解是正数,则a的取值范围是( )A、 B、 C、a为任何实数 D、a为大于0的数9. 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )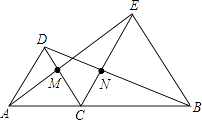 A、3个 B、2个 C、1个 D、0个10. 关于x的不等式组 有四个整数解,则a的取值范围是( )A、 B、 C、 D、
A、3个 B、2个 C、1个 D、0个10. 关于x的不等式组 有四个整数解,则a的取值范围是( )A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. △ABC中, ∠C=90°,若BC=12,AB=13,则AC=12. 某电器商场促销,海尔某型号冰箱的售价是2500元,进价是1800元,商场为保证利润率不低于5%,则海尔该型号冰箱最多降价元.13. △ABC中,如果两条直角边分别为5,12,则斜边上的高线是14. 如图,ΔABC的三边AB,BC,CA的长分别为20,30,40,其三条角平分线将ΔABC分为三个三角形,则SΔABO:SΔBCO:SΔAOC等于。
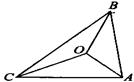 15. 如图,在△ABC 中,AB=AC,AB的中垂线DE交AC于点D,交AB于点E,如果BC=10,△BDC的周长为22,那么AB=
15. 如图,在△ABC 中,AB=AC,AB的中垂线DE交AC于点D,交AB于点E,如果BC=10,△BDC的周长为22,那么AB= 16. 如图,点A是∠MON=45°内部一点,且OA=4cm,分别在边OM,ON上各取一点B,C,分别连接A,B,C三点组成三角形,则ΔABC最小周长为 。
16. 如图,点A是∠MON=45°内部一点,且OA=4cm,分别在边OM,ON上各取一点B,C,分别连接A,B,C三点组成三角形,则ΔABC最小周长为 。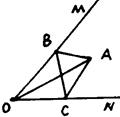
三、简答题(共66分)
-
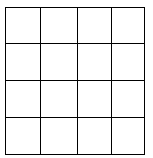
17. 解下列不等式:(1)、(2)、解不等式组18. 在如图4×4所示的网格中,画一个面积为5的等腰直角三角形
 19. 如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
19. 如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.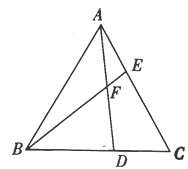 (1)、求证: ≌△CAD;(2)、求∠BFD的度数.20. 工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需要甲种原料9千克,乙种原料3千克;生产一件B 种产品需要甲种原料4千克,乙种原料10千克.则安排A、B两种产品的生产件数有几种方案?21. 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是多少平方厘米?
(1)、求证: ≌△CAD;(2)、求∠BFD的度数.20. 工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需要甲种原料9千克,乙种原料3千克;生产一件B 种产品需要甲种原料4千克,乙种原料10千克.则安排A、B两种产品的生产件数有几种方案?21. 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是多少平方厘米?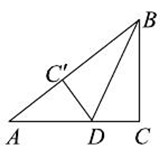 22. 老师请同学在一张长为17cm,宽为16cm的长方形纸板上剪下一个腰长为10cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上)请你帮同学们计算剪下的等腰三角形的面积。23. 如图,在等腰 中,∠C=90°,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持 .连接DE、DF、EF.在此运动变化的过程中,下列结论:求证 是等腰直角三角形;
22. 老师请同学在一张长为17cm,宽为16cm的长方形纸板上剪下一个腰长为10cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上)请你帮同学们计算剪下的等腰三角形的面积。23. 如图,在等腰 中,∠C=90°,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持 .连接DE、DF、EF.在此运动变化的过程中,下列结论:求证 是等腰直角三角形;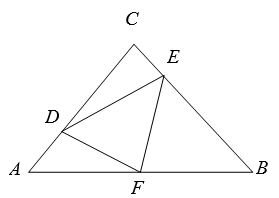 24. 定义:在三角形ABC中,若BC=a,AC=b,AB=c,a,b,c满足,ac+a2=b2则称这个三角形为“类勾股三角形”。请根据以上定义解决下列问题:
24. 定义:在三角形ABC中,若BC=a,AC=b,AB=c,a,b,c满足,ac+a2=b2则称这个三角形为“类勾股三角形”。请根据以上定义解决下列问题: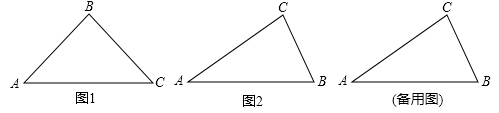 (1)、命题:“直角三角形都是类勾股三角形”是(填“真”或“假”)命题。(2)、如图(a)若等腰三角形ABC“类勾股三角形”,其中AB=BC,AC>AB,请求∠A的度数。(3)、如图(b),在三角形ABC中,∠B=2∠A,且∠C>∠A
(1)、命题:“直角三角形都是类勾股三角形”是(填“真”或“假”)命题。(2)、如图(a)若等腰三角形ABC“类勾股三角形”,其中AB=BC,AC>AB,请求∠A的度数。(3)、如图(b),在三角形ABC中,∠B=2∠A,且∠C>∠A①当∠A=32°时,你能把这个三角形分成两个等腰三角形吗?若能请在(b)图中画出分割线,并标注被分割后的两个等腰三角形的顶角度数;若不能,请说明理由。
②请证明三角形ABC为“勾股类三角形”