陕西省汉中市镇巴县2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
1. 下列是单项式的是( )A、x B、 C、 D、2. 十年来,我国知识产权战略实施取得显著成就,全国著作权登记计量已达到2748000件.将数据2748000用科学记数法表示为( )A、 B、 C、 D、3. 下面的几何体中,主(正)视图为三角形的是( )A、
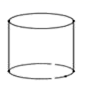 B、
B、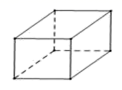 C、
C、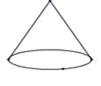 D、
D、 4. 如图,直线 和直线 相交于点 ,若 70°,则 的度数是( )
4. 如图,直线 和直线 相交于点 ,若 70°,则 的度数是( )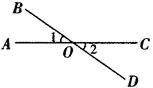 A、100° B、115° C、135° D、145°5. 在 ,在这四个数中,绝对值最小为( )A、4 B、 C、 D、-56. 已知 4则 的值为( )A、-1 B、2 C、-3 D、47. 已知∠A=25.12°,∠B=25°12′,∠C=1528′,那么它们的大小关系为( )A、 B、 C、 D、8. 若a和b互为相反数,且 ,则下列各组中,不是互为相反数的一组是( )A、 和 B、 和 C、 和 D、 和9. 如图是正方体的展开图,原正方体相对两个面上的数字之积的最大值是( )
A、100° B、115° C、135° D、145°5. 在 ,在这四个数中,绝对值最小为( )A、4 B、 C、 D、-56. 已知 4则 的值为( )A、-1 B、2 C、-3 D、47. 已知∠A=25.12°,∠B=25°12′,∠C=1528′,那么它们的大小关系为( )A、 B、 C、 D、8. 若a和b互为相反数,且 ,则下列各组中,不是互为相反数的一组是( )A、 和 B、 和 C、 和 D、 和9. 如图是正方体的展开图,原正方体相对两个面上的数字之积的最大值是( ) A、-12 B、30 C、24 D、2010. 如图,点C是 的中点,点D是 的中点,下列结论:① ;② ;③ ;④ ,正确的有( )
A、-12 B、30 C、24 D、2010. 如图,点C是 的中点,点D是 的中点,下列结论:① ;② ;③ ;④ ,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 用代数式表示“比a的平方小1的数”是.12. 一个多边形有8条边,从其中的一个顶点出发,连接这个点和其他顶点,可以得到 个三角形.13. 点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于14. 如图,AB//CD,直线EF与AB、CD分别交于点G、H,GM⊥GE,∠BGM=20°,HN平分∠CHE,则∠NHD的度数为.

三、解答题
-
15. 计算: .16. 如图,已知线段a、b,用尺规作一条线段c,使c=2a+b.(保留作图痕迹,不写作法)
 17. 已知多项式(1)、把这个多项式按x的降幂重新排列 ;(2)、请指出该多项式的次数,并写出它的二次项和常数项.18. 如图,OA的方向是北偏东15°,OB的方向是西偏北50°,若∠AOC=∠AOB,求OC的方向.
17. 已知多项式(1)、把这个多项式按x的降幂重新排列 ;(2)、请指出该多项式的次数,并写出它的二次项和常数项.18. 如图,OA的方向是北偏东15°,OB的方向是西偏北50°,若∠AOC=∠AOB,求OC的方向. 19. 先化简,再求值: ,其中x=3,y=-2.20. 如图是一些由棱长均为 的小立方块所搭的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.
19. 先化简,再求值: ,其中x=3,y=-2.20. 如图是一些由棱长均为 的小立方块所搭的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数. (1)、请分别画出这个几何体的主视图和左视图;(2)、求这个几何体的体积.21. 已知,有理数a的倒数是它的本身,负数b的绝对值是2,c与2的和的相反数为-1,求 的值.22. 如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.
(1)、请分别画出这个几何体的主视图和左视图;(2)、求这个几何体的体积.21. 已知,有理数a的倒数是它的本身,负数b的绝对值是2,c与2的和的相反数为-1,求 的值.22. 如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.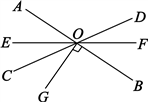 23. 某水果店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下表:(单位:千克)
23. 某水果店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下表:(单位:千克)与标准质量的差值
-3
-2
-1.5
0
+1
+2.5
筐数
1
4
2
3
2
8
(1)、与标准质量比较,这20筐苹果总计超过或不足多少千克?(2)、若苹果每千克售价2元,则出售这20筐苹果可卖多少元?24. 某校发起了“保护流浪动物”行动,七年级两个班的105名学生积极参与,踊跃捐款,已知甲班有 的学生每人捐了10元,乙班有 的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人.(1)、用含x的代数式表示两班捐款的总额;(结果要化简)(2)、计算当x=45,两班共捐款多少元?25. 如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB (1)、若∠B=87°,求∠DCG的度数;(2)、AD与BC是什么位置关系?并说明理由;(3)、若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
(1)、若∠B=87°,求∠DCG的度数;(2)、AD与BC是什么位置关系?并说明理由;(3)、若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.