广西壮族自治区河池市凤山县2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-11-23 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2 + 1$ 的结果是（）

A、3 B、 $- 1$ C、 $- 3$ D、1

查看试题解析
2. 参加国庆70周年阅兵的全体受阅官兵由人民解放军、武警部队和民兵预备役部队月15000名官兵，把15000用科学记数法表示为（）

A、 $15 \times 10^{3}$ B、 $0.15 \times 10^{5}$ C、 $1.5 \times 10^{4}$ D、 $1.5 \times 10^{3}$

查看试题解析
3. 下列各组中的单项式是同类项的是（）

A、 $2 x y^{2}$ 和 $- \frac{1}{2}$ $y^{2}$ $x$ B、 $- m^{2} n p$ 和 $- m n^{2}$ C、 $- m^{2}$ 和 $- 2 m$ D、 $0.5 a$ 和 $- \frac{1}{2} b$

查看试题解析
4.
如图是一个正方体的表面展开图，则原正方体中与“中”字所在的面相对的面上标的字是（　　）

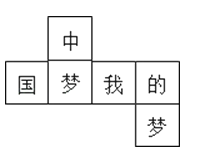A、我 B、的 C、梦 D、国

查看试题解析
5. 在数轴上，到表示 $- 5$ 的点的距离等于5个单位的点所表示的数是（）

A、10 B、 $- 10$ C、0或 $- 10$ D、 $- 10$ 或10

查看试题解析
6. 下列各式计算的结果为正数的是（）

A、 $- 5 + 3$ B、 $- 3^{2}$ C、 ${(- 2)}^{3}$ D、 $- {(- 1)}^{2019}$

查看试题解析
7. 下列计算正确的是（）

A、 $3 a + 2 a = 5 a^{2}$ B、 $- a^{2} b + 2 a^{2} b = a^{2} b$ C、 $2 a^{3} + 3 a^{2} = 5 a^{5}$ D、 $3 a - a = 3$

查看试题解析
8. 已知 $x = 2$ 是关于x的一元一次方程 $a x - 3 = 1$ 的解，则 $a$ 的值为（）

A、4 B、2 C、1 D、 $- 2$

查看试题解析
9. 下列方程变形不正确的是（）

A、 $4 x - 3 = 3 x + 2$ 变形得： $4 x - 3 x = 2 + 3$ B、 $3 x = 2$ 变形得： $x = \frac{2}{3}$ C、 $2 (3 x - 2) = 3 (x + 1)$ 变形得： $6 x - 4 = 3 x + 3$ D、 $\frac{2}{3} x - 1 = \frac{1}{2} x + 3$ 变形得： $4 x - 1 = 3 x + 18$

查看试题解析
10. 如果单项式 $x^{2} y^{m + 2}$ 与 $x^{n} y$ 的和仍然是一个单项式，则 ${(m + n)}^{2019}$ 等于（）

A、1 B、-1 C、2019 D、-2019

查看试题解析
11. 一张试卷有25道选择题，做对一题得4分，做错一题得-1分，某同学做完了25道题，共得70分，那么他做对的题数是（）

A、17道 B、18道 C、19道 D、20道

查看试题解析
12. 如图，下列各图形中的三个数之间均具有相同的规律.根据此规律，图形中M与m、n的关系是

A、M=mn B、M=n(m+1) C、M=mn+1 D、M=m(n+1)

查看试题解析

二、填空题

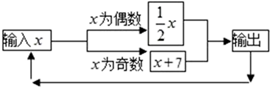
13. 如果收入500元记作 $+ 500$ 元，那么支出200元记作.

查看试题解析
14. 已知： ${(a + 2)}^{2} + | b - 3 | = 0$ ，则 $2 a - b^{2} =$ .

查看试题解析
15. 已知方程（m﹣1）x^|m|＝6是关于x的一元一次方程，则m的值是

查看试题解析
16. 若 $∠ 1 + ∠ 2 = 90^{°}, ∠ 1 + ∠ 3 = 90^{°}$ ，则 $∠ 2 = ∠ 3$ ，其根据是.

查看试题解析
17. 元旦当天，怡佳商场把品牌彩电按标价的8折出售，仍然获利 20% ，若该彩电的进价为3000元，则标价是元.

查看试题解析
18. 如图所示的运算程序中，若开始输入的x值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，则第2019次输出的结果为.

查看试题解析

三、解答题

19. 计算下列各题：

(1)、 $(- 6) \times 8 - 12 \div (- 3) + | - 9 |$

(2)、 $- 8 \times {(- \frac{1}{2})}^{3} + (\frac{3}{4} + \frac{1}{6} - \frac{5}{8}) \div (- \frac{1}{24})$

查看试题解析
20. 解下列方程：

(1)、 $3 (x + 2) - 2 (x + 2) = 2 x + 4$

(2)、 $\frac{x - 1}{2} - \frac{3 x - 1}{4} = 1$

查看试题解析
21. 已知 $| a | = 8, b^{2} = 36$ ，且 $b > a$ ，求 $a + b$ 的值.

查看试题解析
22. 先化简，再求值： $4 x y - (2 x^{2} + 5 x y - y^{2}) + 2 (x^{2} + 3 x y)$ ，其中 $x = - 2$ ， $y = 1$ .

查看试题解析
23. 作图题：根据下列语句，画出图形：

（ 1 ）画直线 $A B$ ；

（ 2 ）连接 $A C ， B D$ ，相交于点O；

（ 3 ）在点B的北偏西 $50^{°}$ 方向且与点B距离为 $2 c m$ 处有一点P，请在图上确定P点的位置.

查看试题解析
24. 如图，将书页的一角斜折过去，使角的顶点A落在 $A^{'}$ 处， $B C$ 为折痕， $B D$ 平分 $∠ A^{'} B E$ .

(1)、求 $∠ C B D$ 的度数.

(2)、若 $∠ A^{'} B E = 120^{°}$ ，求 $∠ C B A$ 的度数.

查看试题解析
25. 某校七年级（1）班想买一些运动器材供班上同学大课间活动使用，班主任安排班长去商店买篮球和排球，下面是班长与售货员的对话：

班长：阿姨，您好！

售货员：同学，你好，想买点什么？

根据这段对话，请你求出篮球和排球的单价各是多少元？

查看试题解析
26. 如图，已知 $A ， B ， C$ 是数轴上的三点，点C表示的数是6， $B C = 4 ， A B = 12$ .

(1)、写出数轴上点A，点B表示的数；

(2)、点M为线段 $A B$ 的中点， $C N = 3$ ，求 $M N$ 的长；

(3)、动点 $P ， Q$ 分别从 $A ， C$ 同时出发，点P以每秒6个单位长度的速度沿数轴向右匀速运动，点Q以每秒3个单位长度的速度沿数轴向左匀速运动，求t为何值时，原点O恰好为线段 $P Q$ 的中点.

查看试题解析