广西壮族自治区桂林市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-11-23 类型：期末考试

进入出卷网下载

一、单选题

1. 2019的相反数是（）

A、2019 B、-2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 下列计算正确的是（　　）

A、 $3 a + 2 b = 5 a b$ B、 $a + a = a^{2}$ C、 $5 a - 3 a = 2$ D、 $3 a - 2 a = a$

查看试题解析
3. 下列采用的调查方式中，不合适的是（　　）

A、为了了解全国中学生的身高状况，采用抽样调查的方式 B、为了了解某型号电子产品的使用寿命情况，采用全面调查的方式 C、为了了解某校九年级三班学生的视力情况，采用全面调查的方式 D、为了了解人们保护水资源的意识，采用抽样调查的方式

查看试题解析
4. 若 $x = 5$ 是方程 $a + x = 8$ 的解，则a的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
5. 若 $∠ A = 60^{°}$ ，则 $∠ A$ 的补角是它余角的（　　）

A、2倍 B、3倍 C、4倍 D、5倍

查看试题解析
6. 数a的绝对值一定是（　　）

A、非负数 B、负数 C、非正数 D、正数

查看试题解析
7. 在数轴上，点A表示的数是 $- 2$ ，点B表示的数是6，则线段 $A B$ 的中点表示的数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
8. 平面上有A，B，C三点，经过任意两点画一条直线，可以画出直线的数量为（　　）

A、1条 B、3条 C、1条或3条 D、无数条

查看试题解析
9. 下列说法正确的是（　　）

A、若 $a = b$ ，则 $a + c = b + c$ B、若 $a c = b c$ ，则 $a = b$ C、若 $a = b$ ，则 $\frac{a}{c} = \frac{b}{c}$ D、若 $a^{2} = b^{2}$ ，则 $a = b$

查看试题解析
10. 甲、乙两水池共储水100吨，若甲池注进水20吨，乙池用去水30吨后，两池所储水量相等，设甲池原来有水x吨，则可列方程如下正确的是（　　）

A、 $x + 20 = (100 - x) + 30$ B、 $x - 20 = (100 - x) + 30$ C、 $x + 20 = (100 - x) - 30$ D、 $x - 20 = (100 - x) - 30$

查看试题解析
11. 如图，B，C两点把线段 $A D$ 分成 $2 ： 4 ： 3$ 的三部分，M是 $A D$ 的中点， $C D = 6$ ，则线段 $B M$ 等于（　　　　）

A、3 B、4 C、5 D、6

查看试题解析
12. 如图，从左至右第1个图由1个正六边形，6个正方形和6个等边三角形组成；第二个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成按此规律，第n个图中正方形和等边三角形的个数之和为（　　）

A、 $(9 n + 3)$ 个 B、 $(6 n + 5)$ 个 C、 $(6 n + 3)$ 个 D、 $(9 n + 5)$ 个

查看试题解析

二、填空题

13. 计算： $- 11 + 9 =$ .

查看试题解析
14. 多项式 $5 x^{3} + 4 x^{2} - 9$ 的次数是.

查看试题解析
15. 一个角的度数是 $28 ° 25^{'}$ ，则它的余角等于.

查看试题解析
16. 已知太阳与地球之间的平均距离约为 $\begin{matrix} 150 & 000 & 000 \end{matrix}$ 千米，用科学记数法表示为千米．

查看试题解析
17. 1930年，德国汉堡大学的学生考拉兹，曾经提出过这样一个数学猜想：对于每一个正整数，如果它是奇数，则对它乘3再加1；如果它是偶数，则对它除以2.如此循环，最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”，又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明，但举例验证都是正确的，例如：取正整数5，最少经过下面5步运算可得1，即： $5 \overset{\times 3 + 1}{\to} 16 \overset{\div 2}{\to} 8 \overset{\div 2}{\to} 4 \overset{\div 2}{\to} 2 \overset{\div 2}{\to} 1$ 如果正整数m最少经过6步运算可得到1，则m的值为.

查看试题解析
18. 当代数式 ${(x - 3)}^{2} + 8$ 取得最小值时，代数式 $x + 4$ 的值是.

查看试题解析

三、解答题

19. 计算：

(1)、 $13 + (- 7) - 5$ ；　　　　

(2)、 ${(- 2)}^{3} \div 4 - | - 5 | - 4 \times (- 2)$

查看试题解析
20. 解下列一元一次方程：

(1)、 $4 x + 3 = 2 x - 7$ 　　　　

(2)、 $\frac{3 x - 1}{2} - \frac{x + 2}{5} = x$

查看试题解析
21. 先化简，再求值： $4 x^{2} - 2 x y + y^{2} - 2 (x^{2} - x y + 5 y^{2})$ ，其中 $x = 3, y = - 1$ .

查看试题解析
22. 如图，已知 $∠ M O N$ ，按下列要求画图.

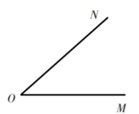
（ 1 ）在 $∠ M O N$ 的内部画射线；

（ 2 ）画 $∠ M O Q$ ，使 $O N$ 在 $∠ M O Q$ 的内部；

（ 3 ）在完成（1）、（2）后，图中共个角.

查看试题解析

23. 某校在校园文化艺术节期间，举办了歌咏、小品、书法、绘画共四个项目的比赛，要求每名学生必须参加且仅参加一项.小明随机调查了部分学生的报名情况，根据调查结果绘制出了如下不完整的“各项目参赛人数及比例”统计表，请根据图表中提供的信息，解答下列的问题：

(1)、本次调查中共抽取了名学生；

(2)、表中的

a =

，

b =

；

(3)、根据统计表中的数据和所学统计图的知识，任选绘制一幅统计图，能直观反映各项目的参加人数或参赛人数的比例.

各项目参赛人数及比例统计表

项目	人数	百分比
歌咏	20	$10 %$
小品	60	a
书法	b	$40 %$
绘画	40	$20 %$

查看试题解析

24. 如图所示， $∠ A O C$ 和 $∠ B O D$ 都是直角.

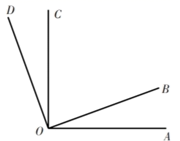(1)、填空：图中与 $∠ B O C$ 互余的角有和；

(2)、 $∠ A O D$ 与 $∠ B O C$ 互补吗？为什么？

(3)、若 $∠ A O B ： ∠ A O D = 3 ： 13$ ，求 $∠ B O C$ 与 $∠ A O D$ 的度数.

查看试题解析
25. 已知A、B两地相距400千米，甲、乙两车从A地向B地运送货物，甲车的速度为每小时60千米，乙车的速度为每小时80千米，甲车先出发0.5小时后乙车才开始出发.

(1)、乙车出发几小时后，才能追上甲车？

(2)、若乙车到达B地后，立即原路返回A地，则乙车返回时再经过多少小时与甲车再次相遇？

查看试题解析
26. 如图，在直线 $A B$ 上，线段 $A B = 24$ ，动点P从A出发，以每秒2个单位长度的速度在直线 $A B$ 上运动. $M$ 为 $A P$ 的中点，N为 $B P$ 的中点，设点P的运动时间为 $t$ 秒.

(1)、若点P在线段 $A B$ 上的运动，当 $P M = 10$ 时， $P N =$ ；

(2)、若点P在射线 $A B$ 上的运动，当 $P M = 2 P N$ 时，求点P的运动时间t的值；

(3)、当点P在线段 $A B$ 的反向延长线上运动时，线段AB、PM、PN有怎样的数量关系？请写出你的结论，并说明你的理由.

查看试题解析