广西玉林市陆川县2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-11-23 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 若 $x = 4$ 是关于x的方程 $\frac{x}{2} - a = 4$ 的解，则a的值为（）

A、－6 B、2 C、16 D、－2

查看试题解析
3.
如图，射线AB与AC所组成的角不正确的表示方法是（　　）

A、∠1 B、∠A C、∠BAC D、∠CAB

查看试题解析
4. 若 $m a = m b ，$ 则下列等式不一定成立的是（）

A、 $a = b$ B、 $m a + 3 = m b + 3$ C、 $- 2 m a = - 2 m b$ D、 $m a - 2 = m b - 2$

查看试题解析
5. 下列关于多项式 $1 - 2 x + \frac{1}{2} x^{2}$ 的说法，错误的是（　　）

A、它是二次多项式 B、它由1，2x， $\frac{1}{2} x^{2}$ 三项组成 C、最高次项的系数是 $\frac{1}{2}$ D、第二项的系数是﹣2

查看试题解析
6. 已知∠α＝12°12′，∠β＝12.12°，∠γ＝12.2°，则下列结论正确的是（　　）

A、∠α＝∠β B、∠α $<$ ∠β C、∠β $>$ ∠γ D、∠α＝∠γ

查看试题解析
7. 已知线段AB=12cm.C是AB的中点.在线段AB上有一点D，且CD=2cm.则AD的长是（）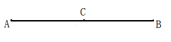

A、8cm B、8cm或 2cm C、8cm或 4cm D、2cm 或 4cm

查看试题解析
8. 如图，∠AOB=70°，射线OC是可绕点O旋转的射线，当∠BOC=15°时，则∠AOC的度数是（）

A、55° B、85° C、55°或85° D、不能确定

查看试题解析
9. 下列说法中：①－a一定是一个负数；②经过两点有一条直线，并且只有一条直线；③一个锐角的补角一定大于它的余角；④绝对值最小的有理数是1；⑤倒数等于它本身的数只有1，正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 甲乙两个超市为了促销一种定价相等的商品，甲超市连续两次降价 $10 ％$ ，乙超市一次性降价 $20 ％$ ，在哪家超市购买同样的商品最合算（）

A、甲 B、乙 C、相同 D、和商品的价格有关

查看试题解析
11. 有m辆客车及n个人，若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则最后一辆车有2个空位.根据题意，列出五个等式：①40m+10=43m﹣2；②40m﹣10=43m+2；③ $\frac{n - 10}{40}$ = $\frac{n + 2}{43}$ ；④ $\frac{n + 10}{40}$ = $\frac{n - 2}{43}$ ；⑤43m=n+2.其中正确的是（　　）

A、②⑤ B、①③④ C、①③⑤ D、②④⑤

查看试题解析
12. 如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB＝ $\frac{1}{2}$ ∠MFE.则∠EFM的度数为（　　）

A、30° B、36° C、45° D、72°

查看试题解析

二、填空题

13. 化简：a﹣2a＝.

查看试题解析
14. 如图，共有条射线.

查看试题解析
15. 若﹣7x^m+2y²与3x³yⁿ是同类项，则m+n＝.

查看试题解析
16. 将一副三角板如图摆放，若∠BAE=135°17′，则∠CAD的度数是．

查看试题解析
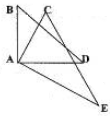17. 如图，点A，B，C，D，E，F都在同一直线上，点B是线段AD的中点，点E是线段CF的中点，有下列结论：①AE＝ $\frac{1}{2}$ （AC+AF），②BE＝ $\frac{1}{2}$ AF，③BE＝ $\frac{1}{2}$ （AF﹣CD），④BC＝ $\frac{1}{2}$ （AC﹣CD）.其中正确的结论是（只填相应的序号）.

查看试题解析
18. 如图图形都是由面积为1的正方形按一定的规律组成，其中，第1个图形中面积为1的正方形有9个，第2个图形中面积为1的正方形有14个，………，按此规律.则第n个图形中面积为1的正方形的个数为

查看试题解析

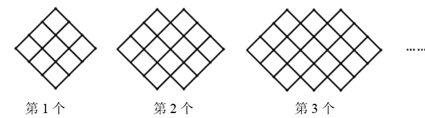
三、解答题

19. 计算或解方程：

(1)、﹣|﹣5|×（﹣1²）﹣4÷（﹣ $\frac{1}{2}$ ）²

(2)、6x+2＝4x﹣6.

(3)、 $x - \frac{1 - x}{3} = \frac{1 - x}{6} - 1$ ，

(4)、 $\frac{1}{2} [x - \frac{1}{2} (x - 1)] = \frac{2}{3} (x - 1 ）$

查看试题解析
20. 化简，再求值：4x²y﹣[6xy﹣2（4xy﹣2﹣x²y）]+1，其中x＝﹣2，y＝1

查看试题解析
21. 一个角的补角加上10°后，等于这个角的余角的3倍，求这个角的余角和补角的度数.

查看试题解析
22. 如图，B，C两点把线段AD分成2∶4∶3的三部分，M是线段AD的中点，CD＝6 cm，求线段MC的长.

查看试题解析
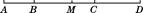23. 同学们，今天我们来学习一个新知识，形如 $| \begin{array}{l} a \\ b \end{array}$ $\begin{array}{l} c \\ d \end{array} |$ 的式子叫做二阶行列式，它的运算法则用公式表示为： $| \begin{array}{l} a \\ b \end{array}$ $\begin{array}{l} c \\ d \end{array} | = a d - b c ，$ 利用此法则解决以下问题：

(1)、仿照上面的解释，计算出 $| \begin{array}{l} 2 \\ - 3 \end{array}$ $\begin{array}{l} 1 \\ 4 \end{array} |$ 的结果；

(2)、依此法则化简 $| \begin{array}{l} - 2 \\ 3 \end{array}$ $\begin{array}{l} a b - 3 a + b \\ 2 a - b - a b \end{array} |$ 的结果；

(3)、如果 $| \begin{array}{l} 5 \\ x + 1 \end{array}$ $\begin{array}{l} 3 \\ x \end{array} | = 4 ，$ 那么 $x$ 的值为多少?

查看试题解析
24. 某班组每天需生产50个零件才能在规定的时间内完成一批零件任务，实际上该班组每天比计划多生产了6个零件，结果比规定的时间提前3天并超额生产120个零件，求该班组原计划要完成的零件任务是多少个？

查看试题解析
25. 如图，OD、OC、OB、OA分别表示东西南北四个方向，OM的方向是西偏北50°，OE的方向是北偏东15°，OE是∠MOG的平分线，∠MOH=∠NOH=90°.

(1)、OH的方向是， ON的方向是；

(2)、通过计算，判断出OG的方向；

(3)、求∠HOG的度数.

查看试题解析
26. 如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB＝10，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t $>$ 0）秒，

(1)、写出数轴上点B所表示的数；

(2)、求线段AP的中点所表示的数（用含t的代数式表示）；

(3)、M是AP的中点，N为PB的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，说明理由；若不变，请你画出图形，并求出线段MN的长.

查看试题解析