浙江省宁波市镇海区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
1. 若3x=2y(xy≠0),则下列比例式成立的是( )A、 B、 C、 D、2. “射击运动员射击一次,命中靶心”这个事件是( )
A、确定事件 B、必然事件 C、不可能事件 D、不确定事件3. 在Rt△ABC中,∠C=90°,∠B=35°,AB=3,则BC的长为( )A、3sin35° B、 C、3cos35° D、3tan35°4. 下列正多边形中,绕其中心旋转72°后,能和自身重合的是( )A、正方形 B、正五边形 C、正六边形 D、正八边形5. 小明沿着坡度为1:2的山坡向上走了10m,则他升高了( )A、5m B、2m C、5m D、10m6. 若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为( )A、144° B、132° C、126° D、108°7. 如图,⊙O是△ABC的外接圆,连接OA、OB,∠C=40°,则∠OAB的度数为( )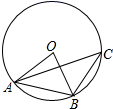 A、30° B、40° C、50° D、80°8. 如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,①∠AED=∠B,② ,③ ,使△ADE与△ACB一定相似( )
A、30° B、40° C、50° D、80°8. 如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,①∠AED=∠B,② ,③ ,使△ADE与△ACB一定相似( )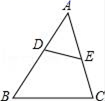 A、①② B、② C、①③ D、①②③9. 如图,在△ABC中,点G为△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,则△ADE与四边形DBCE的面积比为( )
A、①② B、② C、①③ D、①②③9. 如图,在△ABC中,点G为△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,则△ADE与四边形DBCE的面积比为( )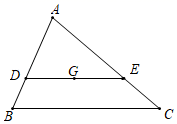 A、 B、 C、 D、10. 如图的 的网格图,A,B,C,D,O都在格点上,点O是( )
A、 B、 C、 D、10. 如图的 的网格图,A,B,C,D,O都在格点上,点O是( ) A、 的外心 B、 的外心 C、 的内心 D、 的内心11. 如图,在▱ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )
A、 的外心 B、 的外心 C、 的内心 D、 的内心11. 如图,在▱ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )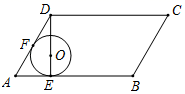 A、2 B、4 C、5﹣ D、8﹣212. 如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为( )
A、2 B、4 C、5﹣ D、8﹣212. 如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为( )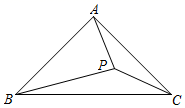 A、0.5 B、 ﹣1 C、2﹣ D、
A、0.5 B、 ﹣1 C、2﹣ D、二、填空题
-
13. 已知 ,则 的值是 .14. 如果在比例尺1:100000的滨海区地图上,招宝山风景区与郑氏十七房的距离约是19cm,则它们之间的实际距离约为千米.15. 二中岗十字路口南北方向的红绿灯设置为:红灯30秒,绿灯60秒,黄灯3秒,小明由南向北经过路口遇到红灯的概率为.16. 如图,一块含30°的直角三角板ABC(∠BAC=30°)的斜边AB与量角器的直径重合,与点D对应的刻度读数是54°,则∠BCD的度数为度.
 17. 如图,扇形ABC的圆心角为90°,半径为6,将扇形ABC绕A点逆时针旋转得到扇形ADE,点B、C的对应点分别为点D、E,若点D刚好落在 上,则阴影部分的面积为.
17. 如图,扇形ABC的圆心角为90°,半径为6,将扇形ABC绕A点逆时针旋转得到扇形ADE,点B、C的对应点分别为点D、E,若点D刚好落在 上,则阴影部分的面积为.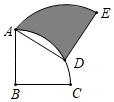 18. 如图,PA与⊙O相切于点A,AB是⊙O的直径,在⊙O上存在一点C满足PA=PC,连结PB、AC相交于点F,且∠APB=3∠BPC,则 =.
18. 如图,PA与⊙O相切于点A,AB是⊙O的直径,在⊙O上存在一点C满足PA=PC,连结PB、AC相交于点F,且∠APB=3∠BPC,则 =.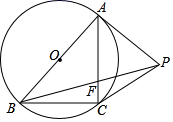
三、解答题
-
19. 计算:2sin30°﹣ cos45°﹣tan230°.20. 两个相似多边形的最长边分别为6cm和8cm,它们的周长之和为56cm,面积之差为28cm2 , 求较小相似多边形的周长与面积.21. 一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.(1)、从袋中随机摸出一个球,记录其颜色,然后放回,搅匀,大量重复该实验,发现摸到绿球的频率稳定于0.2,求n的值;(2)、若 ,小明两次摸球(摸出一球后,不放回,再摸出一球),请用树状图画出小明摸球的所有结果,并求出两次摸出不同颜色球的概率.22. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形.
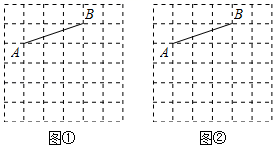
( 1 )在图①中找到两个格点C,使∠BAC是锐角,且tan∠BAC= ;
( 2 )在图②中找到两个格点D,使∠ADB是锐角,且tan∠ADB=1.
23. 如图,O为∠MBN角平分线上一点,⊙O与BN相切于点C,连结CO并延长交BM于点A,过点A作AD⊥BO于点D.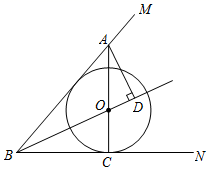 (1)、求证:AB为⊙O的切线;(2)、若BC=6,tan∠ABC= ,求AD的长.24.
(1)、求证:AB为⊙O的切线;(2)、若BC=6,tan∠ABC= ,求AD的长.24.为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
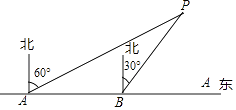 (1)、求∠APB的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?25. 如图,四边形ABCD内接于⊙O,AB是直径,C为 的中点,延长AD,BC交于点P,连结AC.
(1)、求∠APB的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?25. 如图,四边形ABCD内接于⊙O,AB是直径,C为 的中点,延长AD,BC交于点P,连结AC. (1)、求证:AB=AP;(2)、若AB=10,DP=2,
(1)、求证:AB=AP;(2)、若AB=10,DP=2,①求线段CP的长;
②过点D作DE⊥AB于点E,交AC于点F,求△ADF的面积.
26. 定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”. (1)、若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A=度;(2)、如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
(1)、若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A=度;(2)、如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)、如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连结AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.