浙江省宁波市江北区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
1. 成语“水中捞月”所描述的事件是( ).A、必然事件 B、随机事件 C、不可能事件 D、无法确定2. 若2a=5b,则 =( )A、 B、 C、2 D、53. 如图是由6个大小相同的小正方体叠成的几何体,则它的主视图是( )
 A、
A、 B、
B、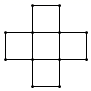 C、
C、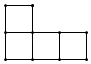 D、
D、 4. ⊙O的半径为5,圆心O到直线l的距离为3,下列位置关系正确的是( )A、
4. ⊙O的半径为5,圆心O到直线l的距离为3,下列位置关系正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 在70周年国庆阅兵式上有两辆阅兵车的车牌号如图所示(每辆阅兵车的车牌号含7位数字或字母),则“9”这个数字在这两辆车牌号中出现的概率为( )
5. 在70周年国庆阅兵式上有两辆阅兵车的车牌号如图所示(每辆阅兵车的车牌号含7位数字或字母),则“9”这个数字在这两辆车牌号中出现的概率为( )
 A、 B、 C、 D、6. 如图,在方格纸中,点A,B,C都在格点上,则tan∠ABC的值是( )
A、 B、 C、 D、6. 如图,在方格纸中,点A,B,C都在格点上,则tan∠ABC的值是( ) A、2 B、 C、 D、7. 如图,在 中, , , 于点D.则 与 的周长之比为( )
A、2 B、 C、 D、7. 如图,在 中, , , 于点D.则 与 的周长之比为( ) A、1:2 B、1:3 C、1:4 D、1:58. 二次函数y=a +bx+c的图象如图所示,则下列关系式错误的是( )
A、1:2 B、1:3 C、1:4 D、1:58. 二次函数y=a +bx+c的图象如图所示,则下列关系式错误的是( ) A、a<0 B、b>0 C、 ﹣4ac>0 D、a+b+c<09. 已知:在△ABC中,∠A=78°,AB=4,AC=6,下列阴影部分的三角形与原△ABC不相似的是( )
A、a<0 B、b>0 C、 ﹣4ac>0 D、a+b+c<09. 已知:在△ABC中,∠A=78°,AB=4,AC=6,下列阴影部分的三角形与原△ABC不相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
10. 如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( ) A、(5,2) B、(2,4) C、(1,4) D、(6,2)11. 如图,⊙O的半径为5,将长为8的线段PQ的两端放在圆周上同时滑动,如果点P从点A出发按逆时针方向滑动一周回到点A,在这个过程中,线段PQ扫过区域的面积为( )
A、(5,2) B、(2,4) C、(1,4) D、(6,2)11. 如图,⊙O的半径为5,将长为8的线段PQ的两端放在圆周上同时滑动,如果点P从点A出发按逆时针方向滑动一周回到点A,在这个过程中,线段PQ扫过区域的面积为( ) A、9π B、16π C、25π D、64π12. 已知二次函数y=﹣x2﹣bx+1(﹣5<b<2),则函数图象随着b的逐渐增大而( )A、先往右上方移动,再往右平移 B、先往左下方移动,再往左平移 C、先往右上方移动,再往右下方移动 D、先往左下方移动,再往左上方移动
A、9π B、16π C、25π D、64π12. 已知二次函数y=﹣x2﹣bx+1(﹣5<b<2),则函数图象随着b的逐渐增大而( )A、先往右上方移动,再往右平移 B、先往左下方移动,再往左平移 C、先往右上方移动,再往右下方移动 D、先往左下方移动,再往左上方移动二、填空题
-
13. 比较三角函数值的大小:sin30°cos30°(填入“>”或“<”).14. 底面半径为1,母线长为2的圆锥的侧面积等于 .15. 抛物线y=(x﹣1)(x﹣3)的对称轴是直线x=.16. 如图,已知在 中, .以 为直径作半圆O,交 于点D.若 ,则 的度数是度.
 17. 如图,在△ABC中,D、E、F分别在AB、AC、BC上,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为.
17. 如图,在△ABC中,D、E、F分别在AB、AC、BC上,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为. 18. 如图,AB为弓形AB的弦,AB=2 ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为.
18. 如图,AB为弓形AB的弦,AB=2 ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为.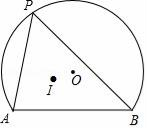
三、解答题
-
19. 计算:20. 2016年3月,我市某中学举行了“爱我中国•朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
 (1)、参加朗诵比赛的学生共有人,并把条形统计图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.21. 已知二次函数y=x2﹣2x﹣3
(1)、参加朗诵比赛的学生共有人,并把条形统计图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.21. 已知二次函数y=x2﹣2x﹣3 (1)、求函数图象的顶点坐标,与坐标轴的交点坐标,并画出函数的大致图象;(2)、根据图象直接回答:当y<0时,求x的取值范围;当y>﹣3时,求x的取值范围.22. 如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,即AQ是⊙O的切线,若∠QAP=α,地球半径为R,
(1)、求函数图象的顶点坐标,与坐标轴的交点坐标,并画出函数的大致图象;(2)、根据图象直接回答:当y<0时,求x的取值范围;当y>﹣3时,求x的取值范围.22. 如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,即AQ是⊙O的切线,若∠QAP=α,地球半径为R,
求:
(1)、航天飞机距地球表面的最近距离AP的长;(2)、P、Q两点间的地面距离,即 的长.(注:本题最后结果均用含α,R的代数式表示)23. 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. (1)、求证:DE是⊙O的切线;(2)、若DE=6cm,AE=3cm,求⊙O的半径.24.
(1)、求证:DE是⊙O的切线;(2)、若DE=6cm,AE=3cm,求⊙O的半径.24. (1)、如图1,在平行四边形ABCD中,点E1 , E2是AB三等分点,点F1 , F2是CD三等分点,E1F1 , E2F2分别交AC于点G1 , G2 , 求证:AG1=G1G2=G2C.(2)、如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)25. 每年十月的第二个周四是世界爱眼日,为预防近视,超市决定对某型号护眼台灯进行降价销售.降价前,进价为30元的护眼台灯以80元售出,平均每月能售出200盏,调查表明:这种护眼台灯每盏售价每降低1元,其月平均销售量将增加10盏.(1)、写出月销售利润y(单位:元)与销售价x(单位:元/盏)之间的函数表达式;(2)、当销售价定为多少元时,所得月利润最大?最大月利润为多少元?26.
(1)、如图1,在平行四边形ABCD中,点E1 , E2是AB三等分点,点F1 , F2是CD三等分点,E1F1 , E2F2分别交AC于点G1 , G2 , 求证:AG1=G1G2=G2C.(2)、如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)25. 每年十月的第二个周四是世界爱眼日,为预防近视,超市决定对某型号护眼台灯进行降价销售.降价前,进价为30元的护眼台灯以80元售出,平均每月能售出200盏,调查表明:这种护眼台灯每盏售价每降低1元,其月平均销售量将增加10盏.(1)、写出月销售利润y(单位:元)与销售价x(单位:元/盏)之间的函数表达式;(2)、当销售价定为多少元时,所得月利润最大?最大月利润为多少元?26.
问题提出:
如图1,在等边△ABC中,AB=9,⊙C半径为3,P为圆上一动点,连结AP,BP,求AP+ BP的最小值
(1)、尝试解决:为了解决这个问题,下面给出一种解题思路,通过构造一对相似三角形,将 BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
如图2,连结CP,在CB上取点D,使CD=1,则有
又∵∠PCD=∠
△∽△
∴
∴PD= BP
∴AP+ BP=AP+PD
∴当A,P,D三点共线时,AP+PD取到最小值
请你完成余下的思考,并直接写出答案:AP+ BP的最小值为.
(2)、自主探索:如图3,矩形ABCD中,BC=6,AB=8,P为矩形内部一点,且PB=4,则 AP+PC的最小值为.(请在图3中添加相应的辅助线)
(3)、拓展延伸:如图4,在扇形COD中,O为圆心,∠COD=120°,OC=4.OA=2,OB=3,点P是 上一点,求2PA+PB的最小值,画出示意图并写出求解过程.