浙江省宁波市慈溪市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-11-23 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，从左边的等边三角形到右边的等边三角形，经过下列一次变化不能得到的是(　　)

A、轴对称 B、平移 C、绕某点旋转 D、先平移再轴对称

查看试题解析
2. 如图所示，若△ABC∽△DEF，则∠E的度数为（）

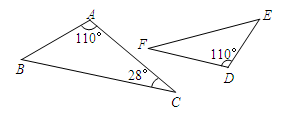A、28° B、32° C、42° D、52°

查看试题解析
3. 下列事件中是随机事件的是(　　)

A、校运会上立定跳远成绩为10米 B、在只装有5个红球的袋中，摸出一个红球 C、慈溪市明年五一节是晴天 D、在标准大气压下，气温3℃ 时，冰熔化为水

查看试题解析
4. 如图，⊙O中，点D，A分别在劣弧BC和优弧BC上，∠BDC=130°，则∠BOC=(　　)

A、120° B、110° C、105° D、100°

查看试题解析
5. 在Rt△ABC中，∠C=90°，AB=5，AC=3，则下列等式正确的是(　　)

A、sinA= $\frac{3}{5}$ B、cosA= $\frac{3}{5}$ C、tanA= $\frac{3}{5}$ D、cosA= $\frac{4}{5}$

查看试题解析
6. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

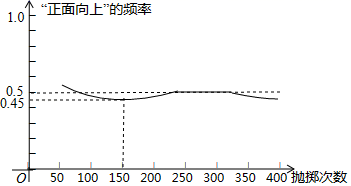
下面有三个推断：

①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；

②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；

③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．

其中合理的是（　　）

A、① B、② C、①② D、①③

查看试题解析
7. 下列命题是真命题的是(　　)

A、在同圆或等圆中，等弧所对的圆周角相等 B、平分弦的直径垂直于弦 C、在同圆或等圆中，等弦所对的圆周角相等 D、三角形外心是三条角平分线的交点

查看试题解析
8. 在平面直角坐标系中，把抛物线y=2x²绕原点旋转180°，再向右平移1个单位，向下平移2个单位，所得的抛物线的函数表达式为(　　)

A、y=2(x﹣1)²﹣2 B、y=2(x+1)²﹣2 C、y=﹣2(x﹣1)²﹣2 D、y=﹣2(x+1)²﹣2

查看试题解析
9. 如图，在△ABC中，D，E，F分别为BC，AB，AC上的点，且EF∥BC，FD∥AB，则下列各式正确的是(　　)

A、 $\frac{A E}{E B} = \frac{C D}{B D}$ B、 $\frac{E F}{B C} = \frac{A E}{D F}$ C、 $\frac{E F}{B C} = \frac{D F}{A B}$ D、 $\frac{A E}{A B} = \frac{B D}{B C}$

查看试题解析
10. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知 $E F = C D = 4$ ，则球的半径长是（）

A、2 B、2.5 C、3 D、4

查看试题解析
11. 已知，当﹣1≤x≤2时，二次函数y=m(x﹣1)²﹣5m+1(m≠0，m为常数)有最小值6，则m的值为(　　)

A、﹣5 B、﹣1 C、﹣1.25 D、1

查看试题解析
12. 如图，已知，M，N分别为锐角∠AOB的边OA，OB上的点，ON=6，把△OMN沿MN折叠，点O落在点C处，MC与OB交于点P，若MN=MP=5，则PN=（）

A、2 B、3 C、 $\frac{8}{3}$ D、 $\frac{10}{3}$

查看试题解析

二、填空题

13. 写出一个图象的顶点在原点，开口向下的二次函数的表达式.

查看试题解析
14. 若两个相似三角形的周长比为2：3，则它们的面积比是．

查看试题解析
15. 已知，⊙O的半径为6，若它的内接正n边形的边长为6 $\sqrt{2}$ ，则n=.

查看试题解析
16. 如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，则大厅两层之间的高度为米．（结果保留两个有效数字）（参考数据；sin31°=0.515，cos31°=0.857，tan31°=0.601）

查看试题解析
17. 如图，⊙O过正方形网格中的格点A，B，C，D，点E也为格点，连结BE交⊙O于点F，P为 $\hat{C D}$ 上的任一点，则tanP=.

查看试题解析
18. 若二次函数的图象与x轴的两个交点和顶点构成等边三角形，则称这样的二次函数的图象为标准抛物线.如图，自左至右的一组二次函数的图象T₁ ， T₂ ， T₃……是标准抛物线，且顶点都在直线y= $\frac{\sqrt{3}}{3}$ x上，T₁与x轴交于点A₁(2，0)，A₂(A₂在A₁右侧)，T₂与x轴交于点A₂ ， A₃ ， T₃与x轴交于点A₃ ， A₄ ， ……，则抛物线T_n的函数表达式为.

查看试题解析

三、解答题

19. 解下列两题：

(1)、已知 $\frac{a}{b} = \frac{3}{4}$ ，求 $\frac{2 a + 3 b}{a}$ 的值；

(2)、已知α为锐角，且2 $\sqrt{3}$ sinα=4cos30°﹣tan60°，求α的度数.

查看试题解析
20. 如图，转盘A中的4个扇形的面积相等，转盘B中的3个扇形面积相等.小明设计了如下游戏规则：甲、乙两人分别任意转动转盘A、B一次，当转盘停止转动时，将指针所落扇形中的2个数相乘，如果所得的积是偶数，那么是甲获胜；如果所得的积是奇数，那么是乙获胜.这样的规则公平吗？为什么？

查看试题解析
21. 如图是四个全等的小矩形组成的图形，这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)

(1)、若每个小矩形的较短边长为1，则BC=；

(2)、①在图1、图2中分别画一个格点三角形(顶点是格点的三角形)，使它们都与△ABC相似(但不全等)，且图1，2中所画三角形也不全等).
②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹，点M用黑点表示，并注上字母M)

查看试题解析
22. 如图，二次函数y=ax²+bx+c过点A(﹣1，0)，B(3，0)和点C(4，5).

(1)、求该二次函数的表达式及最小值.

(2)、点P(m，n)是该二次函数图象上一点.
①当m=﹣4时，求n的值；

②已知点P到y轴的距离不大于4，请根据图象直接写出n的取值范围.

查看试题解析
23. 如图1，是一种自卸货车.如图2是货箱的示意图，货箱是一个底边AB水平的矩形，AB=8米，BC=2米，前端档板高DE=0.5米，底边AB离地面的距离为1.3米.卸货时，货箱底边AB的仰角α=37°(如图3)，求此时档板最高点E离地面的高度.(精确到0.1米，参考值：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)

查看试题解析
24. 某商品市场销售抢手，其进价为每件80元，售价为每件130元，每个月可卖出500件；据市场调查，若每件商品的售价每上涨1元，则每个月少卖2件(每件售价不能高于240元).设每件商品的售价上涨x元(x为正整数)，每个月的销售利润为y元.

(1)、求y与x的函数关系式，并直接写出自变量x的取值范围；

(2)、每件商品的涨价多少元时，每个月可获得最大利润？最大的月利润是多少元？

(3)、每件商品的涨价多少元时，每个月的利润恰为40000元？根据以上结论，请你直接写出x在什么范围时，每个月的利润不低于40000元？

查看试题解析
25. 定义：连结菱形的一边中点与对边的两端点的线段把它分成三个三角形，如果其中有两个三角形相似，那么称这样的菱形为自相似菱形.

(1)、判断下列命题是真命题，还是假命题？
①正方形是自相似菱形；

②有一个内角为60°的菱形是自相似菱形.

③如图1，若菱形ABCD是自相似菱形，∠ABC=α(0°＜α＜90°)，E为BC中点，则在△ABE，△AED，△EDC中，相似的三角形只有△ABE与△AED.

(2)、如图2，菱形ABCD是自相似菱形，∠ABC是锐角，边长为4，E为BC中点.
①求AE，DE的长；

②AC，BD交于点O，求tan∠DBC的值.

查看试题解析
26. 如图，AB是半圆O的直径，C为半圆弧上一点，在AC上取一点D，使BC=CD，连结BD并延长交⊙O于E，连结AE，OE交AC于F.

(1)、求证：△AED是等腰直角三角形；

(2)、如图1，已知⊙O的半径为 $\sqrt{5}$ .
①求 $\hat{C E}$ 的长；

②若D为EB中点，求BC的长.

(3)、如图2，若AF：FD=7：3，且BC=4，求⊙O的半径.

查看试题解析