浙江省嘉兴市2019-2020学年九年级上学期期末数学试题

试卷更新日期：2020-11-23 类型：月考试卷

进入出卷网下载

一、单选题

1. 二次函数y=（x﹣1）²+2，它的图象顶点坐标是（）

A、（﹣2，1） B、（2，1） C、（2，﹣1） D、（1，2）

查看试题解析
2. 若 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{5}{3}$ C、 $\frac{3}{5}$ D、 $\frac{3}{2}$

查看试题解析

3. 对一批衬衣进行抽检，统计合格衬衣的件数，得到合格衬衣的频数表如下：

抽取件数	50	100	150	200	500	800	1000
合格频数	42	88	141	176	448	720	900

估计出售2000件衬衣，其中次品大约是（）

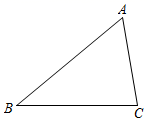
A、50件 B、100件 C、150件 D、200件

查看试题解析

4. 下列说法正确的是（）

A、所有菱形都相似 B、所有矩形都相似 C、所有正方形都相似 D、所有平行四边形都相似

查看试题解析
5. 如图，小明在打乒乓球时，为使球恰好能过网（设网高AB＝15cm），且落在对方区域桌子底线C处，已知小明在自己桌子底线上方击球，则他击球点距离桌面的高度DE为（）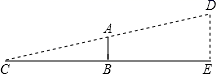

A、15cm B、20cm C、25cm D、30cm

查看试题解析
6. 如图，点A，B，C在⊙O上，则下列结论正确的是（）

A、∠AOB＝∠ACB B、∠AOB＝2∠ACB C、∠ACB的度数等于 $\overset{⌢}{A B}$ 的度数 D、∠AOB的度数等于 $\frac{1}{2}$ $\overset{⌢}{A B}$ 的度数

查看试题解析
7. 如图，在△ABC中，中线AD、BE相交于点F，EG∥BC，交AD于点G，则 $\frac{A G}{A F}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
8. 一副三角板（△ABC与△DEF）如图放置，点D在AB边上滑动，DE交AC于点G，DF交BC于点H，且在滑动过程中始终保持DG＝DH，若AC＝2，则△BDH面积的最大值是（）

A、3 B、3 $\sqrt{3}$ C、 $\frac{3}{2}$ D、 $\frac{3 \sqrt{3}}{2}$

查看试题解析
9. 如图，一张扇形纸片OAB，∠AOB＝120°，OA＝6，将这张扇形纸片折叠，使点A与点O重合，折痕为CD，则图中未重叠部分（即阴影部分）的面积为（）

A、9 $\sqrt{3}$ B、12π﹣9 $\sqrt{3}$ C、 $\frac{9}{2} \sqrt{3}$ D、6π﹣ $\frac{9}{2} \sqrt{3}$

查看试题解析
10. 如图，二次函数y＝ax²+bx+c的图象与x轴相交于A，B两点，C(m，﹣3)是图象上的一点，且AC⊥BC，则a的值为（）

A、2 B、 $\frac{1}{2}$ C、3 D、 $\frac{1}{3}$

查看试题解析

二、填空题

11. 线段 $a = 2$ ， $b = 3$ 的比例中项是.

查看试题解析
12. 将二次函数y＝x²﹣6x+8化成y＝a（x+m）²+k的形式是.

查看试题解析
13. 如图，C、D是AB为直径的半圆O上的点，若∠BAD＝50°，则∠BCD＝.

查看试题解析
14. 有两辆车按1，2编号，舟舟和嘉嘉两人可任意选坐一辆车.则两人同坐2号车的概率为.

查看试题解析
15. 已知一个扇形的半径为5cm，面积是20cm² ，则它的弧长为.

查看试题解析
16. 如图，等腰△ABC中，∠A＝36°，AB＝AC，BD平分∠ABC交AC于点D，则 $\frac{C D}{A D}$ 的值等于.

查看试题解析
17. 一个半径为5cm的球形容器内装有水，若水面所在圆的直径为8cm，则容器内水的高度为cm.

查看试题解析
18. 定义符号max{a，b}的含义为：当a≥b时，max{a，b}＝a；当a＜b时，max{a，b}＝b.如max{1，﹣3}＝1，则max{x²+2x+3，﹣2x+8}的最小值是.

查看试题解析
19. 如图，一组等距的平行线，点A、B、C分别在直线l₁、l₆、l₄上，AB交l₃于点D，AC交l₃于点E，BC交于l₅点F，若△DEF的面积为1，则△ABC的面积为.

查看试题解析
20. 已知二次函数y＝x²﹣bx（b为常数），当2≤x≤5时，函数y有最小值﹣1，则b的值为.

查看试题解析

三、解答题

21. 已知抛物线 $y = x^{2} + b x + c$ 的图象经过点（﹣1，0），点（3，0）；

(1)、求抛物线函数解析式；

(2)、求函数的顶点坐标.

查看试题解析
22. 在一个不透明的盒子里装有4个标有1，2，3，4的小球，它们形状、大小完全相同.小明从盒子里随机取出一个小球，记下球上的数字，作为点P的横坐标x，放回然后再随机取出一个小球，记下球上的数字，作为点P的纵坐标y.

(1)、画树状图或列表，写出点P所有可能的坐标；

(2)、求出点P在以原点为圆心，5为半径的圆上的概率.

查看试题解析
23. 如图，BC是半圆O的直径，D是弧AC的中点，四边形ABCD的对角线AC、BD交于点E.

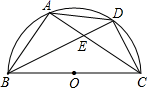(1)、求证：△DCE∽△DBC；

(2)、若CE= $\sqrt{5}$ ，CD=2，求直径BC的长.

查看试题解析
24. 某童装店购进一批20元/件的童装，由销售经验知，每天的销售量y（件）与销售单价x（元）之间存在如图的一次函数关系.

(1)、求y与x之间的函数关系；

(2)、当销售单价定为多少时，每天可获得最大利润，最大利润是多少？

查看试题解析
25. 如图，已知△ABC，∠A＝60°，AB＝6，AC＝4.

(1)、用尺规作△ABC的外接圆O；

(2)、求△ABC的外接圆O的半径；

(3)、求扇形BOC的面积.

查看试题解析
26. 如图，抛物线y＝﹣x²+4x+m﹣4（m为常数）与y轴交点为C，M(3，0)、N(0，﹣2)分别是x轴、y轴上的点.

(1)、求点C的坐标（用含m的代数式表示）；

(2)、若抛物线与x轴有两个交点A、B，是否存在这样的m，使得线段AB＝MN，若存在，求出m的值，若不存在，请说明理由；

(3)、若抛物线与线段MN有公共点，求m的取值范围.

查看试题解析