陕西省延安市延长县2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-11-23 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y = - 2 {(x - 2)}^{2} + 3$ 的顶点坐标是（）

A、 $(- 2, 3)$ B、 $(2, - 3)$ C、 $(- 2, - 3)$ D、 $(2, 3)$

查看试题解析
2. 关于x的一元二次方程x²﹣（k+3）x+2k+2＝0的根的情况，下面判断正确的是（　　）

A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、无实数根

查看试题解析
3. 如图，图1是由5个完全相同的正方体堆成的几何体，现将标有E的正方体平移至如图2所示的位置，下列说法中正确的是（）

A、左、右两个几何体的主视图相同 B、左、右两个几何体的左视图相同 C、左、右两个几何体的俯视图不相同 D、左、右两个几何体的三视图不相同

查看试题解析
4. 如图，在矩形ABCD中，AB＝4，BC＝6，将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF，延长DA交FG于点H，则GH的长为（　　）

A、8﹣4 $\sqrt{3}$ B、 $\frac{8 \sqrt{3}}{3}$ ﹣4 C、3 $\sqrt{3}$ ﹣4 D、6﹣3 $\sqrt{3}$

查看试题解析
5. 在平面直角坐标系中，抛物线 $y = (x + 5) (x - 3)$ 经过变换后得到抛物线 $y = (x + 3) (x - 5)$ ，则这个变换可以是（）

A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位

查看试题解析
6. 在反比例函数y＝ $\frac{k - 2}{x}$ 图象的每一条曲线上，y都随x的增大而增大，则k的取值范围是（）

A、k＞2 B、k＞0 C、k≥2 D、k＜2

查看试题解析
7. 如图，已知直线a∥b∥c ，直线m、n与a、b、c分别交于点A、C、E、B、D、F ，若AC＝8，CE＝12，BD＝6，则BF的值是（）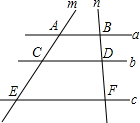

A、14 B、15 C、16 D、17

查看试题解析
8. 如图，BC是⊙O的弦，OA⊥BC，∠AOB=55°，则∠ADC的度数是（　　）

A、25° B、55° C、45° D、27.5°

查看试题解析
9. 如图，在⊙O中，AB⊥OC，垂足为点D，AB＝8，CD＝2，若点P是优弧 $\overset{⌢}{AmB}$ 上的任意一点，则sin∠APB＝（　　）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{1}{2}$

查看试题解析
10. 如果点A（﹣5，y₁），B（﹣ $\frac{7}{2}$ ，y₂），C（ $\frac{3}{2}$ ，y₃），在双曲线y＝ $\frac{k}{x}$ 上（k＜0），则y₁ ， y₂ ， y₃的大小关系是（）

A、y₃＜y₁＜y₂ B、y₂＜y₁＜y₃ C、y₁＜y₂＜y₃ D、y₁＜y₃＜y₂

查看试题解析
11. 如图，平面直角坐标系中，点E（﹣4，2），F（﹣1，﹣1），以原点O为位似中心，把△EFO缩小为△E′F′O ，且△E′F′O与△EFO的相似比为1：2，则点E的对应点E′的坐标为（　　）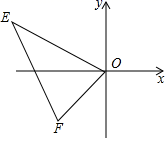

A、（2，﹣1） B、（8，﹣4） C、（2，﹣1）或（﹣2，1） D、（8，﹣4）或（﹣8，4）

查看试题解析
12. 二次函数 $y = {ax}^{2} + bx + c$ 的图象如图所示，反比例函数 $y = \frac{b}{x}$ 与一次函数 $y = cx + a$ 在同一平面直角坐标系中的大致图象是

A、 B、 C、 D、

查看试题解析

二、填空题

13. 计算： $2 \sqrt{2}$ sin45°·cos30°+3tan60°= .

查看试题解析
14. 正五边形的中心角的度数是．

查看试题解析
15. 用配方法解方程 $\frac{1}{2} x^{2} + x - \frac{5}{2} = 0$ 时，可配方为 $\frac{1}{2} [{(x + 1)}^{2} + k] = 0$ ，其中 $k =$ .

查看试题解析
16. 已知小明身高 $1.8 m$ ，在某一时刻测得他站立在阳光下的影长为 $0.6 m$ .若当他把手臂竖直举起时，测得影长为 $0.78 m$ ，则小明举起的手臂超出头顶 $m$ .

查看试题解析
17. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ，且 $D E$ 把 $△ A B C$ 分成面积相等的两部分.若 $A D = 4$ ，则 $D B$ 的长为.

查看试题解析
18. 如图，由四个全等的直角三角形围成的大正方形ABCD的面积为34，小正方形EFGH的面积为4，则tan∠DCG的值为.

查看试题解析
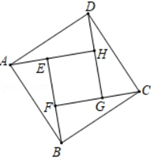19. 如图，⊙O经过A，B，C三点，PA，PB分别与⊙O相切于A，B点，∠P＝46°，则∠C＝.

查看试题解析
20. 如图，已知在矩形ABCD中，AB＝2，BC＝3，P是线段AD上的一动点，连接PC，过点P作PE⊥PC交AB于点E.以CE为直径作⊙O，当点P从点A移动到点D时，对应点O也随之运动，则点O运动的路程长度为.

查看试题解析

三、解答题

21. 小明和小亮两人一起玩投掷一个普通正方体骰子的游戏.

(1)、说出游戏中必然事件，不可能事件和随机事件各一个；

(2)、如果两个骰子上的点数之积为奇数，小明胜，否则小亮胜，你认为这个游戏公平吗？如果不公平，谁获胜的可能性较大？请说明理由.请你为他们设计一个公平的游戏规则.

查看试题解析
22. 学校打算用长 $16$ 米的篱笆围城一个长方形的生物园饲养小兔，生物园的一面靠在长为 $8$ 米的墙上（如图）.

(1)、若生物园的面积为 $30$ 平方米，求生物园的长和宽；

(2)、能否围城面积为 $35$ 平方米的生物园？若能，求出长和宽；若不能，请说明理由.

查看试题解析
23. 如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需要绕行B地，已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长（结果保留整数）（参考数据：sin67°≈0.92；cos67°≈0.38； $\sqrt{3}$ ≈1.73）

查看试题解析
24. 如图，在平面直角坐标系中，过点M（0，2）的直线l与x轴平行，且直线l分别与反比例函数y＝ $\frac{6}{x}$ （x＞0）和y＝ $\frac{k}{x}$ （x＜0）的图象分别交于点P，Q.

(1)、求P点的坐标；

(2)、若△POQ的面积为9，求k的值.

查看试题解析
25. 如图（1），某数学活动小组经探究发现：在⊙O中，直径AB与弦CD相交于点P，此时PA· PB=PC·PD

(1)、如图（2），若AB与CD相交于圆外一点P，上面的结论是否成立？请说明理由.

(2)、如图（3），将PD绕点P逆时针旋转至与⊙O相切于点C，直接写出PA、PB、PC之间的数量关系.

(3)、如图（3），直接利用（2）的结论，求当 PC= $\sqrt{3}$ ，PA=1时，阴影部分的面积.

查看试题解析
26. 在平面直角坐标系xOy中，抛物线y＝x²+bx+c交x轴于A（﹣1，0），B（3，0）两点，交y轴于点C.

(1)、如图1，求抛物线的解析式；

(2)、如图2，点P是第一象限抛物线上的一个动点，连接CP交x轴于点E，过点P作PK∥x轴交抛物线于点K，交y轴于点N，连接AN、EN、AC，设点P的横坐标为t，四边形ACEN的面积为S，求S与t之间的函数关系式（不要求写出自变量t的取值范围）；

(3)、如图3，在（2）的条件下，点F是PC中点，过点K作PC的垂线与过点F平行于x轴的直线交于点H，KH＝CP，点Q为第一象限内直线KP下方抛物线上一点，连接KQ交y轴于点G，点M是KP上一点，连接MF、KF，若∠MFK＝∠PKQ，MP＝AE+ $\frac{5}{12}$ GN，求点Q坐标.

查看试题解析