陕西省延安市洛川县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
1. 关于x的一元二次方程x2+mx﹣1=0的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定
-
2. 对于二次函数y=2(x﹣1)2﹣3,下列说法正确的是( )A、图象开口向下 B、图象和y轴交点的纵坐标为﹣3 C、x<1时,y随x的增大而减小 D、图象的对称轴是直线x=﹣1
-
3. 如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是( )
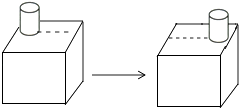 A、主视图 B、左视图 C、俯视图 D、主视图和俯视图
A、主视图 B、左视图 C、俯视图 D、主视图和俯视图 -
4. 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )
 A、110° B、120° C、150° D、160°
A、110° B、120° C、150° D、160° -
5. 在平面直角坐标系中,抛物线 经过变换后得到抛物线 ,则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位
-
6. 在双曲线 的每一分支上,y都随x的增大而增大,则k的值可以是( )A、2 B、3 C、0 D、1
-
7. 如图,已知AD∥BE∥CF,那么下列结论不成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 如图,BC是⊙O的弦,OA⊥BC,∠AOB=55°,则∠ADC的度数是( )
 A、25° B、55° C、45° D、27.5°
A、25° B、55° C、45° D、27.5° -
9. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
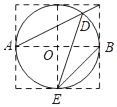 A、 B、 C、2 D、
A、 B、 C、2 D、 -
10. 在平面直角坐标系中,点E(﹣4,2),点F(﹣1,﹣1),以点O为位似中心,按比例1:2把△EFO缩小,则点E的对应点E的坐标为( )A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,4) C、(2,﹣1) D、(8,﹣4)
-
11. 如果点A(﹣5,y1),B(﹣ ,y2),C( ,y3),在双曲线y= 上(k<0),则y1 , y2 , y3的大小关系是( )A、y3<y1<y2 B、y2<y1<y3 C、y1<y2<y3 D、y1<y3<y2
-
12.
二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为( )
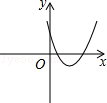 A、
A、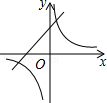 B、
B、 C、
C、 D、
D、
二、填空题
-
13. cos30°+ sin45°+tan60°=.
-
14. 一元二次方程x2﹣x﹣ =0配方后可化为.
-
15. 在上午的某一时刻身高1.7米的小刚在地面上的影长为3.4米,同时一棵树在地面上的影子长12米,则树的高度为米.
-
16. 如图,已知△ABC,D,E分别在AB,AC边上,且DE∥BC,AD=2,DB=3,△ADE面积是4,则四边形DBCE的面积是.

-
17. 如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则cosα=.

-
18. 如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数 位于第一象限的图象上,则k的值为.

-
19. 如图,△ABC是⊙O的内接三角形,∠A=120°,过点C的圆的切线交BO于点P,则∠P的度数为.

-
20. 如图,一个长为4,宽为3的长方形木板斜靠在水平桌面上的一个小方块上,其长边与水平桌面成30°夹角,将长方形木板按逆时针方向做两次无滑动的翻滚,使其长边恰好落在水平桌面l上,则木板上点A滚动所经过的路径长为.

三、解答题
-
21. 如图,一次函数的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.

根据以往所学的函数知识以及本题的条件,你能提出求解什么问题?并解决这些问题(至少三个问题).
-
22. 在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)、“从中任意抽取1个球不是红球就是白球”是事件,“从中任意抽取1个球是黑球”是事件;(2)、从中任意抽取1个球恰好是红球的概率是;
(3)、学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
-
23. 某商店以每件40元的价格进了一批商品,出售价格经过两个月的调整,从每件50元上涨到每件72元,此时每月可售出188件商品.(1)、求该商品平均每月的价格增长率;(2)、因某些原因,商家需尽快将这批商品售出,决定降价出售.经过市场调查发现:售价每下降一元,每个月多卖出一件,设实际售价为x元,则x为多少元时销售此商品每月的利润可达到4000元.
-
24. 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
 (1)、求点C到直线AB的距离;
(1)、求点C到直线AB的距离;
(2)、求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
-
25.

图(1) 图(2) 图(3)
如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
(1)、如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.(2)、如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.(3)、如图(3),直接利用(2)的结论,求当 PC= ,PA=1时,阴影部分的面积. -
26. 如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
 (1)、求抛物线的解析式;(2)、点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
(1)、求抛物线的解析式;(2)、点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
