陕西省咸阳市秦都区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
1. 已知函数 的图象过点 ,则该函数的图象必在( )A、第二、三象限 B、第二、四象限 C、第一、三象限 D、第三、四象限2. 一个物体如图所示,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,已知AB∥CD∥EF,AC=4,CE=1,BD=3,则DF的值为( )
3. 如图,已知AB∥CD∥EF,AC=4,CE=1,BD=3,则DF的值为( ) A、 B、 C、 D、14. 小亮同学在教学活动课中,用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )A、线段 B、三角形 C、平行四边形 D、正方形5. 如图,已知 若 的面积为 ,则 的面积为( )
A、 B、 C、 D、14. 小亮同学在教学活动课中,用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )A、线段 B、三角形 C、平行四边形 D、正方形5. 如图,已知 若 的面积为 ,则 的面积为( ) A、 B、 C、 D、6. 如图,在矩形 中, 于F,则线段 的长是( )
A、 B、 C、 D、6. 如图,在矩形 中, 于F,则线段 的长是( )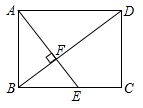 A、 B、 C、 D、7. 若关于x的一元二次方程 有两个相等的实数根,则k的值为( )A、 B、 C、 D、8. 为了迎接春节,某厂10月份生产春联 万幅,计划在12月份生产春联 万幅,设11、12月份平均每月增长率为x,根据题意,可列出方程为( )A、 B、 C、 D、9. 如图,在菱形 中, ,且 连接 则 ( )
A、 B、 C、 D、7. 若关于x的一元二次方程 有两个相等的实数根,则k的值为( )A、 B、 C、 D、8. 为了迎接春节,某厂10月份生产春联 万幅,计划在12月份生产春联 万幅,设11、12月份平均每月增长率为x,根据题意,可列出方程为( )A、 B、 C、 D、9. 如图,在菱形 中, ,且 连接 则 ( ) A、 B、 C、 D、10. 若反比例函数 图象上有两个点 ,设 ,则 不经过第( )象限.A、一 B、二 C、三 D、四
A、 B、 C、 D、10. 若反比例函数 图象上有两个点 ,设 ,则 不经过第( )象限.A、一 B、二 C、三 D、四二、填空题
-
11. 为了估计抛掷同一枚啤酒瓶盖落地后凸面向上的概率,小明做了大量重复试验.经过统计发现共抛掷 次啤酒瓶盖,凸面向上的次数为 次,由此可估计抛掷这枚啤酒瓶盖落地后凸面向上的概率约为(结果精确到 )12. 如果关于x的一元二次方程 的一个根是 则 .13. 如图,在矩形 中,对角线 与 相交于点O, ,垂足为点E, ,且 ,则 的长为.
 14. 如图,已知两个反比例函数 和 在第一象限内的图象,设点P在 上, 轴于点 交 于点 轴于点D,交 于点B,则四边形 的面积为.
14. 如图,已知两个反比例函数 和 在第一象限内的图象,设点P在 上, 轴于点 交 于点 轴于点D,交 于点B,则四边形 的面积为.
三、解答题
-
15. 解方程:x2+10x+9=0.16. 如图,AB、CD、EF是与路灯在同一直线上的三个等高的标杆,已知AB、CD在路灯光下的影长分别为BM、DN,在图中作出EF的影长.
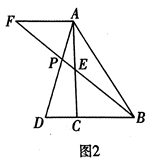
 17. 如图, 是 的角平分线,延长 至点 使得 .求证: .
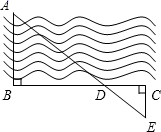
17. 如图, 是 的角平分线,延长 至点 使得 .求证: . 18. 如图所示的双曲线是函数 为常数, )图象的一支若该函数的图象与一次函数 的图象在第一象限的交点为 ,求点A的坐标及反比例函数的表达式.
18. 如图所示的双曲线是函数 为常数, )图象的一支若该函数的图象与一次函数 的图象在第一象限的交点为 ,求点A的坐标及反比例函数的表达式.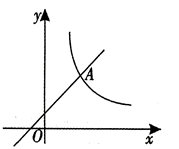 19. 李明从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15立方米的无盖长方体运输箱,且此长方体运输箱底面的长比宽多2米,现已知购买这种铁皮每平方米需20元,问购买这张矩形铁皮共花了多少钱?20. 如图,正方形 的对角线 、 相交于点O,过点B作 的平行线,过点C作 的平行线,它们相交于点E.求证:四边形 是正方形.
19. 李明从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15立方米的无盖长方体运输箱,且此长方体运输箱底面的长比宽多2米,现已知购买这种铁皮每平方米需20元,问购买这张矩形铁皮共花了多少钱?20. 如图,正方形 的对角线 、 相交于点O,过点B作 的平行线,过点C作 的平行线,它们相交于点E.求证:四边形 是正方形. 21. 某校举行田径运动会,学校准备了某种气球,这些全球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V( )的反比例函数,其图象如图所示:
21. 某校举行田径运动会,学校准备了某种气球,这些全球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V( )的反比例函数,其图象如图所示: (1)、求这个函数的表达式;(2)、当气球内的气压大于150 kPa时,气球将会爆炸,为了安全起见,气体的体积应至少是多少?22. 《厉害了,我的国》是在央视财经频道的纪录片《辉煌中国》的基础上改编而成的电影记录了过去五年以来中国桥、中国路、中国车、中国港、中国网等超级工程的珍贵影像.小明和小红都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定谁去看电影,规则如下:在一个不透明的袋子中装有编号为 的四个球(除编号外都相同),小明从中随机摸出一个球,记下数字后放回,小红再从中摸出一个球,记下数字,若两次数字之和大于 则小明获得电影票,若两次数字之和小于 则小红获得电影票.(1)、请用列表或画树状图的方法表示出两数和的所有可能的结果;(2)、分别求出小明和小红获得电影票的概率.23. 如图,为了估算河的宽度,在河对岸选定一个目标作为点A再在河的这边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
(1)、求这个函数的表达式;(2)、当气球内的气压大于150 kPa时,气球将会爆炸,为了安全起见,气体的体积应至少是多少?22. 《厉害了,我的国》是在央视财经频道的纪录片《辉煌中国》的基础上改编而成的电影记录了过去五年以来中国桥、中国路、中国车、中国港、中国网等超级工程的珍贵影像.小明和小红都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定谁去看电影,规则如下:在一个不透明的袋子中装有编号为 的四个球(除编号外都相同),小明从中随机摸出一个球,记下数字后放回,小红再从中摸出一个球,记下数字,若两次数字之和大于 则小明获得电影票,若两次数字之和小于 则小红获得电影票.(1)、请用列表或画树状图的方法表示出两数和的所有可能的结果;(2)、分别求出小明和小红获得电影票的概率.23. 如图,为了估算河的宽度,在河对岸选定一个目标作为点A再在河的这边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.