陕西省渭南市富平县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
1. 计算 的值是( )A、 B、 C、 D、2. 下列图形的主视图与左视图不相同的是( )A、
 B、
B、 C、
C、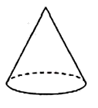 D、
D、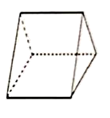 3. 若点 在反比例函数 上,则 的值是( )A、 B、 C、 D、4. 如图:已知 ,且 ,则 ( )
3. 若点 在反比例函数 上,则 的值是( )A、 B、 C、 D、4. 如图:已知 ,且 ,则 ( ) A、5 B、3 C、3. 2 D、45. 小明在太阳光下观察矩形木板的影子,不可能是( )A、平行四边形 B、矩形 C、线段 D、梯形6. 若关于x的一元二次方程 有两个相等的根,则b的值为( )A、 B、 C、 或 D、 或7. 如图,在Rt△ABC中,∠ACB=900 , CD⊥AB于点D,BC=3,AC=4,tan∠BCD的值为( )
A、5 B、3 C、3. 2 D、45. 小明在太阳光下观察矩形木板的影子,不可能是( )A、平行四边形 B、矩形 C、线段 D、梯形6. 若关于x的一元二次方程 有两个相等的根,则b的值为( )A、 B、 C、 或 D、 或7. 如图,在Rt△ABC中,∠ACB=900 , CD⊥AB于点D,BC=3,AC=4,tan∠BCD的值为( ) A、 ; B、 ; C、 ; D、 ;8. 如图,矩形ABCD中,连接AC,延长BC至点E,使 ,连接DE.若 ,则∠E的度数是( )
A、 ; B、 ; C、 ; D、 ;8. 如图,矩形ABCD中,连接AC,延长BC至点E,使 ,连接DE.若 ,则∠E的度数是( ) A、65° B、60° C、50° D、40°9. 已知点 都在反比例函数 为常数,且 )的图象上,则 与 的大小关系是( )A、 B、 C、 D、10. 如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )
A、65° B、60° C、50° D、40°9. 已知点 都在反比例函数 为常数,且 )的图象上,则 与 的大小关系是( )A、 B、 C、 D、10. 如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )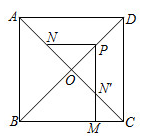 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 小明练习射击,共射击 次,其中有 次击中靶子,由此可估计,小明射击一次击中靶子的概率约为.12. 已知 是一元二次方程 的一个解,则m的值是.13. 如图,P(m,m)是反比例函数 在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为.
 14. 如图,O为Rt△ABC斜边中点,AB=10,BC=6,M、N在AC边上,若△OMN∽△BOC,点M的对应点是O,则CM=.
14. 如图,O为Rt△ABC斜边中点,AB=10,BC=6,M、N在AC边上,若△OMN∽△BOC,点M的对应点是O,则CM=.
三、解答题
-
15. 解方程:3x(2x+1)=4x+2.16. 如图,在边长为 个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).请在网格中画出△ABC以A为位似中心放大到原来的 倍的格点△AB1C1 , 并写出△ABC与△AB1C1 , 的面积比(△ABC与△AB1C1 , 在点A的同一侧)
 17. 如图所示,请画出这个几何体的三视图.
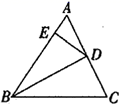
17. 如图所示,请画出这个几何体的三视图. 18. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.
18. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.证明:△BCD∽△BDE.
 19. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
19. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F. (1)、求证:四边形AECF是矩形;(2)、连接OE,若AE=4,AD=5,求OE的长.20. 如图,在宽为40 m,长为64 m的矩形地面上,修筑三条同样宽的道路,每条道路均与矩形地面的一条边平行,余下的部分作为耕地,要使得耕地的面积为2418 m2 , 则道路的宽应为多少?
(1)、求证:四边形AECF是矩形;(2)、连接OE,若AE=4,AD=5,求OE的长.20. 如图,在宽为40 m,长为64 m的矩形地面上,修筑三条同样宽的道路,每条道路均与矩形地面的一条边平行,余下的部分作为耕地,要使得耕地的面积为2418 m2 , 则道路的宽应为多少? 21. 李师傅驾驶出租车匀速地从西安市送客到咸阳国际机场,全程约 ,设小汽车的行驶时间为t (单位:h),行驶速度为v(单位: ),且全程速度限定为不超过 .(1)、求v关于t的函数表达式;(2)、李师傅上午 点驾驶小汽车从西安市出发.需在 分钟后将乘客送达咸阳国际机场,求小汽车行驶速度v.22. 富平因取“富庶太平”之意而得名,是华夏文明重要发祥地之一.某班举行关于“美丽的富平”的演讲活动.小明和小丽都想第一个演讲,于是他们通过做游戏来决定谁第一个来演.讲游戏规则是:在一个不透明的袋子中有一个黑球a和两个白球b、c,(除颜色外其它均相同),小丽从袋子中摸出一个球,放回后搅匀,小明再从袋子中摸出一个球,若两次摸到的球颜色相同,则小丽获胜,否则小明获胜,请你用树状图或列表的方法分别求出小丽与小明获胜的概率,并说明这个游戏规则对双方公平吗?23. 大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列人第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为 米的标杆 ,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上) ,这时测得 米, 米,请你根据以上数据,计算古塔的高度 .
21. 李师傅驾驶出租车匀速地从西安市送客到咸阳国际机场,全程约 ,设小汽车的行驶时间为t (单位:h),行驶速度为v(单位: ),且全程速度限定为不超过 .(1)、求v关于t的函数表达式;(2)、李师傅上午 点驾驶小汽车从西安市出发.需在 分钟后将乘客送达咸阳国际机场,求小汽车行驶速度v.22. 富平因取“富庶太平”之意而得名,是华夏文明重要发祥地之一.某班举行关于“美丽的富平”的演讲活动.小明和小丽都想第一个演讲,于是他们通过做游戏来决定谁第一个来演.讲游戏规则是:在一个不透明的袋子中有一个黑球a和两个白球b、c,(除颜色外其它均相同),小丽从袋子中摸出一个球,放回后搅匀,小明再从袋子中摸出一个球,若两次摸到的球颜色相同,则小丽获胜,否则小明获胜,请你用树状图或列表的方法分别求出小丽与小明获胜的概率,并说明这个游戏规则对双方公平吗?23. 大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列人第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为 米的标杆 ,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上) ,这时测得 米, 米,请你根据以上数据,计算古塔的高度 . 24. 如图是一种简易台灯的结构图,灯座为△ABC,A、C、D在同一直线上,量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB的距离).(结果取整,参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27, ≈1.73)
24. 如图是一种简易台灯的结构图,灯座为△ABC,A、C、D在同一直线上,量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB的距离).(结果取整,参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27, ≈1.73) 25. 从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)、如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线.
25. 从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)、如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线. (2)、在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.(3)、如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.
(2)、在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.(3)、如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.