陕西省宝鸡市凤翔县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-23 类型:期末考试
一、单选题
-
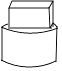
1. 如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )
 A、
A、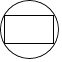 B、
B、 C、
C、 D、
D、 2. 顺次连接矩形各边中点得到的四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形3. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
2. 顺次连接矩形各边中点得到的四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形3. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )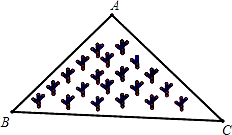 A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点4. 如上图, ,直线a,b与 、 、 分别相交于A、B、C和点D、E、F.若 , ,则 的长是( )
A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点4. 如上图, ,直线a,b与 、 、 分别相交于A、B、C和点D、E、F.若 , ,则 的长是( )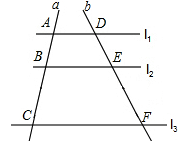 A、 B、6 C、6.3 D、10.55. 如下图要测量小河两岸相对的两点P、A的距离,可以在小河边取 的垂线 上的一点C,测得 米, ,则小河宽 为( )
A、 B、6 C、6.3 D、10.55. 如下图要测量小河两岸相对的两点P、A的距离,可以在小河边取 的垂线 上的一点C,测得 米, ,则小河宽 为( )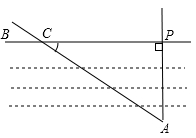 A、 米 B、 米 C、 米 D、 米6. 如图,在 中 . . 是 的角平分线.若在边 上截取 ,连接 ,则图中等腰三角形共有( )
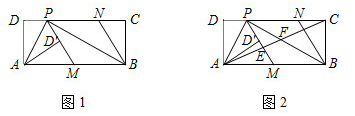
A、 米 B、 米 C、 米 D、 米6. 如图,在 中 . . 是 的角平分线.若在边 上截取 ,连接 ,则图中等腰三角形共有( )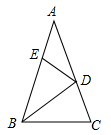 A、3个 B、5个 C、6个 D、2个7. 一个布袋内只装有1个黑球和2个白球,这些球除颜色不同外其余都相同,随机摸出一个球后放回搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )A、 B、 C、 D、8. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )
A、3个 B、5个 C、6个 D、2个7. 一个布袋内只装有1个黑球和2个白球,这些球除颜色不同外其余都相同,随机摸出一个球后放回搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )A、 B、 C、 D、8. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )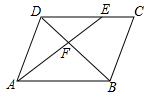 A、 B、 C、 D、9. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )A、
A、 B、 C、 D、9. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )A、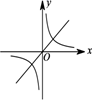 B、
B、 C、
C、 D、
D、 10. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点.若AM=2,则线段ON的长为( )
10. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点.若AM=2,则线段ON的长为( )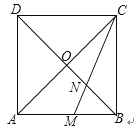 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
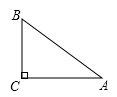
11. 在 中, , , ,则 的长是.
 12. 一元二次方程x2=2x的解为.13. 若一个反比例函数的图象经过点 和 ,则这个反比例函数的表达式为.14. 如图,在菱形 中, , ,点P,Q,K分别为线段 , , 上的任意一点,则 的最小值为.
12. 一元二次方程x2=2x的解为.13. 若一个反比例函数的图象经过点 和 ,则这个反比例函数的表达式为.14. 如图,在菱形 中, , ,点P,Q,K分别为线段 , , 上的任意一点,则 的最小值为.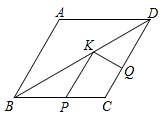
三、解答题
-
15. 解方程(1)、(2)、16. 如图,已知在正方形ABCD中,M是BC边上一定点,连接AM,请用尺规作图法,在AM上求作一点P,使得△DPA∽△ABM(不写做法保留作图痕迹)
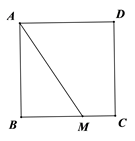 17. 某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵树的产量就会减少2个,但多种的桃树不能超过100棵,如果要使产量增加15.2%,那么应多种多少棵桃树?18. 如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
17. 某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵树的产量就会减少2个,但多种的桃树不能超过100棵,如果要使产量增加15.2%,那么应多种多少棵桃树?18. 如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.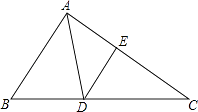 (1)、求证:△DCE∽△BCA;(2)、若AB=3,AC=4.求DE的长.19. 现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。(1)、将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;(2)、小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。20. 小明开着汽车在平坦的公路上行驶,前方出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
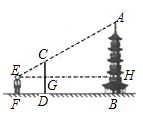
(1)、求证:△DCE∽△BCA;(2)、若AB=3,AC=4.求DE的长.19. 现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。(1)、将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;(2)、小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。20. 小明开着汽车在平坦的公路上行驶,前方出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.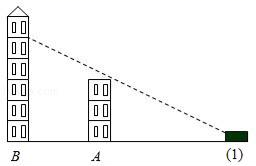 (1)、请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.(2)、若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)21. 如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面 ,竹标顶端离地面 ,小明到竹杆的距离 ,竹杆到塔底的距离 ,求这座古塔的高度.
(1)、请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.(2)、若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)21. 如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面 ,竹标顶端离地面 ,小明到竹杆的距离 ,竹杆到塔底的距离 ,求这座古塔的高度.