陕西省宝鸡市陈仓区2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-11-23 类型：期末考试

进入出卷网下载

一、单选题

1. 已知x=2是一元二次方程x²+mx+2=0的一个解，则m的值是（）

A、﹣3 B、3 C、0 D、0或3

查看试题解析
2. 方程x²＝4x的解是（）

A、x＝0 B、x₁＝4，x₂＝0 C、x＝4 D、x＝2

查看试题解析
3. 下列对正方形的描述错误的是（　　）

A、正方形的四个角都是直角 B、正方形的对角线互相垂直 C、邻边相等的矩形是正方形 D、对角线相等的平行四边形是正方形

查看试题解析
4. 如图是由5个大小相同的正方体组成的几何体，它的俯视图为（）

A、 B、 C、 D、

查看试题解析
5. 如图，在▱ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，若BG= $4 \sqrt{2}$ ，则△CEF的面积是（）

A、 $2 \sqrt{2}$ B、 $\sqrt{2}$ C、 $3 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
6. 关于x的方程 $x^{2} - 2 x + k = 0$ 有两个不相等的实数根，则k的取值范围是（　　）

A、k＜1 B、k＞1 C、k＜－1 D、k＞－1

查看试题解析
7. 如图，在 $Δ A B C$ 中， $D E / / B C$ ， $A D ： A B = 1 ： 3$ ， $S_{Δ A D E} ： S_{四边形 D E B C}$ 等于（）

A、 $1 ： 3$ B、 $1 ： 8$ C、 $1 ： 9$ D、 $1 ： 4$

查看试题解析
8. 为执行“两免一补”政策，某地区2006年投入教育经费2500万元，预计2008年投入3600万元．设这两年投入教育经费的年平均增长百分率为x，则下列方程正确的是（　　）

A、2500x²=3600 B、2500（1+x）²=3600 C、2500（1+x%）²=3600 D、2500（1+x）+2500（1+x）²=3600

查看试题解析
9. 在一个不透明的布袋中，有红色、黑色、白色球共40个，它们除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在 $15 %$ 和 $45 %$ ，则布袋中白色球的个数可能是（）

A、24 B、18 C、16 D、6

查看试题解析
10. 如图，直线l和双曲线 $y = \frac{k}{x} (k > 0)$ 交于A，B两点，P是线段 $A B$ 上的点（不与A，B重合），过点A，B，P分别向x轴作垂线，垂足分别是C，D，E，连接 $O A$ ， $O B$ ， $O P$ ，设 $Δ A O C$ 面积是 $S_{1}$ ， $Δ B O D$ 面积是 $S_{2}$ ， $Δ P O E$ 面积是 $S_{3}$ ，则（）.

A、 $S_{1} < S_{2} < S_{3}$ B、 $S_{1} > S_{2} > S_{3}$ C、 $S_{1} = S_{2} > S_{3}$ D、 $S_{1} = S_{2} < S_{3}$

查看试题解析

二、填空题

11. 某商品经过连续两次降价，销售单价由原来的125元降到80元，则平均每次降价的百分率为．

查看试题解析
12. 小明身高1.8m，王鹏身高1.50m，他们在同一时刻站在阳光下，小明影子长为1.20m，则王鹏的影长为m．

查看试题解析
13. 菱形的两条对角线长分别是方程 $x^{2} - 14 x + 48 = 0$ 的两实根，则菱形的面积为．

查看试题解析
14. 反比例函数的图象与经过原点的直线相交于点A，B，已知A点的坐标是 $(2, 1)$ ，那么B点的坐标为.

查看试题解析
15. 如图，△ABC中，DE垂直平分AC交AB于E，∠A=30°，∠ACB=80°，则∠BCE=°.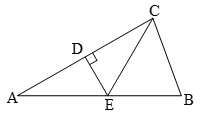

查看试题解析
16. 直线 $l_{1}$ ： $y = k_{1} x + b$ 与双曲线 $l_{2}$ ： $y = \frac{k_{2}}{x}$ 在同一平面直角坐标系中的图象如图所示，则关于x的不等式 $\frac{k_{2}}{x} > k_{1} x + b$ 的解集为.

查看试题解析

三、解答题

17. 解方程:

(1)、 $x^{2} - 4 x + 1 = 0$ ；

(2)、 ${(x - 3)}^{2} + 4 x (x - 3) = 0$ .

查看试题解析
18. 如图，已知 $Δ A B C$ ，请用尺规作图，过点A作一条直线 $A D$ ，使其交 $B C$ 于点D，且使 $Δ A B C \sim Δ D A C$ .（保留作图痕迹，不写作法）

查看试题解析
19. 已知关于x的方程x²－（m＋2）x＋（2m－1）=0。

(1)、求证：方程恒有两个不相等的实数根；

(2)、若此方程的一个根是1，请求出方程的另一个根，并求以此两根为边长的直角三角形的周长。

查看试题解析
20. 如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．

(1)、请你在图中画出旗杆在同一时刻阳光照射下形成的影子；

(2)、如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．

查看试题解析
21. 九年级（1）班要从甲乙两名同学中选派一人去参加学校举行的”扫黑除恶”知识竞赛，王老师准备用一副扑克牌中排列数字分别为 $3$ ， $4$ ， $5$ ， $6$ 的四张扑克牌做抽数字游戏，决定谁去参加比赛，游戏规则为；将这四张牌的正面全部朝下，洗匀后从中随机抽取一张，得到的数字作为十位上的数字，然后将所抽到的牌放回，再从中随机抽取一张，得到的数字作为个位上的数字，这样就得到了一个两位数，若这个两位数小于 $50$ ，则甲胜，否则乙获胜，且游戏的获胜者将去参加比赛.

(1)、求抽取的扑克牌使得十位数字是 $5$ 的概率；

(2)、你认为这个游戏公平吗？请运用概率知识说明理由.

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ，D为边 $B C$ 上一点，以 $A B ， B D$ 为邻边作平行四边形 $A B D E$ ，连接 $A D$ ， $E C$ .

(1)、求证： $△ A D C$ ≌ $△ E C D$ ；

(2)、若 $B D = C D$ ，求证：四边形 $A D C E$ 是矩形.

查看试题解析
23. 如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为 $(2 ， 3)$ .双曲线 $y = \frac{k}{x} (x > 0)$ 的图象经过BC的中点D，且与AB交于点E，连接DE.

(1)、求k的值及点E的坐标；

(2)、若点F是OC边上一点，且△FBC∽△DEB，求直线FB的解析式.

查看试题解析