浙江省绍兴市柯桥区2020届九年级上学期数学期末考试试卷
试卷更新日期：2020-11-23 类型：期末考试
一、单选题
-
1. 若 ，则下列比例式中正确的是（ ）A、 B、 C、 D、2. 下列事件中，是随机事件的是（ ）A、三角形任意两边之和大于第三边 B、任意选择某一电视频道，它正在播放新闻联播 C、a是实数，|a|≥0 D、在一个装着白球和黑球的袋中摸球，摸出红球3. 已知⊙O的半径为4cm，点P在⊙O上，则OP的长为（ ）A、2cm B、4cm C、6cm D、8cm4. 如图，△ABC的顶点A，B，C均在⊙O上，若∠ABC+∠AOC＝75°，则∠OAC的大小是（ ）
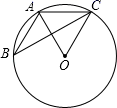A、25° B、50° C、65° D、75°5.如图，线段AB两个端点坐标分别为A（4，6），B（6，2），以原点O为位似中心，在第三象限内将线段AB缩小为原来的后，得到线段CD，则点C的坐标为（ ）
A、（﹣2，﹣3） B、（﹣3，﹣2） C、（﹣3，﹣1） D、（﹣2，﹣1）6. 如图，点G是△ABC的重心，下列结论中正确的个数有（ ）① ；② ；③△EDG∽△CBG；④ ．
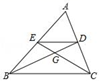A、1个 B、2个 C、3个 D、4个7. 点C为线段AB的黄金分割点，且AC＞BC，下列说法正确的有（ ）①AC= AB，②AC= AB，③AB:AC=AC:BC，④AC≈0.618AB
A、1个 B、2个 C、3个 D、4个8. 如图，将边长为6的正六边形铁丝框ABCDEF（面积记为S1）变形为以点D为圆心，CD为半径的扇形（面积记为S2），则S1与S2的关系为（ ）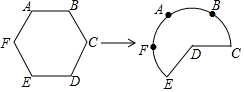
A、S1＝ S2 B、S1＜S2 C、S1＝S2 D、S1＞S29. 若抛物线y＝x2+ax+b与x轴两个交点间的距离为4，称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x＝2，将此抛物线向左平移2个单位，再向上平移3个单位，得到的抛物线过点（ ）A、（1，0） B、（1，8） C、（1，﹣1） D、（1，﹣6）10. 如图坐标系中，O（0，0），A（3，3 ），B（6，0），将△OAB沿直线CD折叠，使点A恰好落在线段OB上的点E处，若OE＝ ，则AC：AD的值是（ ）
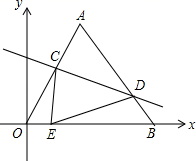A、1：2 B、2：3 C、6：7 D、7：8二、填空题
-
11. 抛物线y＝（x﹣1）2﹣2与y轴的交点坐标是.12. 计算：2sin245°﹣tan45°＝.13. 如图，直线l1∥l2∥l3 ， 直线AC交l1 ， l2 ， l3于点A，B，C； 直线DF交l1 ， l2 ， l3 ， 于点D，E，F，已知 ，则 = ．
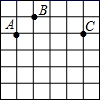
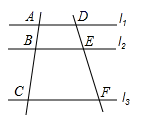14. 如图，点A，B，C均在
的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为.
15. 如图，扇形OAB中，∠AOB＝60°，OA＝4，点C为弧AB的中点，D为半径OA上一点，点A关于直线CD的对称点为E，若点E落在半径OA上，则OE＝.
16. 如图，抛物线y＝﹣ （x+1）（x﹣9）与坐标轴交于A、B、C三点，D为顶点，连结AC，BC.点P是该抛物线在第一象限内上的一点.过点P作y轴的平行线交BC于点E，连结AP交BC于点F，则 的最大值为.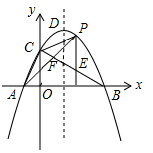
三、解答题
-
17. 一个不透明的袋子中装有3个标号分别为1、2、3的完全相同的小球，随机地摸出一个小球不放回，再随机地摸出一个小球.(1)、采用树状图或列表法列出两次摸出小球出现的所有可能结果；(2)、求摸出的两个小球号码之和等于4的概率.18. 港珠澳大桥是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图，为了测得海豚塔斜拉索顶端A距离海平面的高度，先测出斜拉索底端C到桥塔的距离（CD的长）约为100米，又在C点测得A点的仰角为30°，测得B点的俯角为20°，求斜拉索顶端A点到海平面B点的距离（AB的长）.（已知 ≈1.732，tan20°≈0.36，结果精确到0.1）
19. 如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC.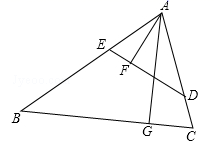
(1)、求证：△ADE∽△ABC；(2)、若AD=3，AB=5，求
的值. 20. 如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，D为弧AC的中点，E是BA延长线上一点，∠DAE＝105°.
(1)、求∠CAD的度数；(2)、若⊙O的半径为4，求弧BC的长.21. 我国互联网发展走到了世界的前列，尤其是电子商务，据市场调查，天猫超市在销售一种进价为每件40元的护眼台灯中发现：每月销售量y（件）与销售单价x（元）之间的函数关系如图所示：
(1)、当销售单价定为50元时，求每月的销售件数；(2)、设每月获得的利润为W（元），求利润的最大值；(3)、由于市场竞争激烈，这种护眼灯的销售单价不得高于75元，如果要每月获得的利润不低于8000元，那么每月的成本最少需要多少元？（成本＝进价×销售量）22. 如图①，是一张直角三角形纸片，∠B＝90°，AB＝12，BC＝8，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大.
(1)、请通过计算说明小明的猜想是否正确；(2)、如图②，在△ABC中，BC＝10，BC边上的高AD＝10，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，求矩形PQMN面积的最大值；(3)、如图③，在五边形ABCDE中，AB＝16，BC＝20，AE＝10，CD＝8，∠A＝∠B＝∠C＝90°.小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积.23. 如图，直线y＝﹣x+3与x轴、y轴分别交于B、C两点，抛物线y＝﹣x2+bx+c经过B、C两点，与x轴另一交点为A，顶点为D.
(1)、求抛物线的解析式；(2)、在x轴上找一点E，使△EDC的周长最小，求符合条件的E点坐标；(3)、在抛物线的对称轴上是否存在一点P，使得∠APB＝∠OCB？若存在，求出PB2的值；若不存在，请说明理由.24. 已知：在⊙O中，弦AC⊥弦BD，垂足为H，连接BC，过点D作DE⊥BC于点E，DE交AC于点F
(1)、如图1，求证：BD平分∠ADF；(2)、如图2，连接OC，若AC＝BC，求证：OC平分∠ACB；(3)、如图3，在（2）的条件下，连接AB，过点D作DN∥AC交⊙O于点N，若AB＝3 ，DN＝9.求sin∠ADB的值.