江苏省海安市九校2021届九年级上学期数学第一次月考试卷

试卷更新日期：2020-11-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列说法错误的是（　　）

A、长度相等的两条弧是等弧 B、直径是圆中最长的弦 C、面积相等的两个圆是等圆 D、半径相等的两个半圆是等弧

查看试题解析
3. 用配方法解方程 $x^{2} + 8 x + 9 = 0$ ，变形后的结果正确的是（）

A、 ${(x + 4)}^{2} = - 9$ B、 ${(x + 4)}^{2} = - 7$ C、 ${(x + 4)}^{2} = 25$ D、 ${(x + 4)}^{2} = 7$

查看试题解析
4. 某中学组织初三学生篮球比赛，以班为单位，每两班之间都比赛一场，计划安排15场比赛，则共有多少个班级参赛？（）

A、4 B、5 C、6 D、7

查看试题解析
5. 如图，在⊙O中，直径EF⊥CD，垂足为M，若CD=2 $\sqrt{5}$ ，EM=5，则⊙O的半径为（）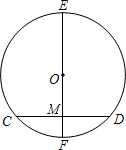

A、2 B、3 C、4 D、6

查看试题解析
6. 点 $A (m - 1, - 2)$ 与点 $B (3, n + 1)$ 关于原点对称，则 $m + n =$ （　　）

A、1 B、-1 C、-5 D、5

查看试题解析
7. 已知关于x的一元二次方程x²+2x+a﹣1=0有两根为x₁和x₂ ，且x₁²﹣x₁x₂=0，则a的值是

A、a=1 B、a=1或a=﹣2 C、a=2 D、a=1或a=2

查看试题解析
8. 已知函数 $y = x^{2} - 2 m x + 2020$ （m为常数）的图象上有三点 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ ， $C (x_{3}, y_{3})$ ，其中 $x_{1} = \sqrt{2} + m$ ， $x_{2} = \frac{2}{3} + m$ ， $x_{3} = m - 1$ ，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（　　）

A、 $y_{2} < y_{3} < y_{1}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
9. 如图，已知二次函数 $y = {ax}^{2} + bx + c (a \neq 0)$ 的图象如图所示，有下列5个结论 $① abc > 0$ ； $② b - a > c$ ； $③ 4 a + 2 b + c > 0$ ； $④ 3 a > - c$ ； $⑤ a + b > m (am + b) (m \neq 1$ 的实数 $) .$ 其中正确结论的有 $($ $)$

A、 $① ② ③$ B、 $② ③ ⑤$ C、 $② ③ ④$ D、 $③ ④ ⑤$

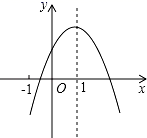查看试题解析
10. 如图，在Rt△ABC 中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF.下列结论：①∠EAF=45°； ②BE=CD；③EA平分∠CEF； ④ $B E^{2} + D C^{2} = D E^{2}$ ，其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知关于x的一元二次方程（m﹣2）x²+2x+1＝0有实数根，则m的取值范围是.

查看试题解析
12. 如图，已知A，B，C，D是⊙O上的点，∠1＝∠2，则下列结论中正确的有个.
① $\overset{⌢}{A B} = \overset{⌢}{C D}$ ；② $\overset{⌢}{D B} = \overset{⌢}{C A}$ ；③AC＝BD；④∠BOD＝∠AOC.

查看试题解析
13. 飞机着陆后滑行的距离y（单位：m）关于滑行时间t（单位：s）的函数解析式是y=60t﹣ $\frac{3}{2} t^{2}$ ．在飞机着陆滑行中，最后4s滑行的距离是m．

查看试题解析
14. 如图，在平面直角坐标系中，点 $A (0 ， 2)$ ， $B (2 \sqrt{3} ， 0)$ ，点P为线段AB的中点，将线段AB绕点O逆时针旋转后点P的对应点P'的坐标是.

查看试题解析
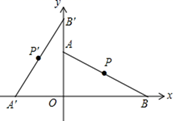15. 二次函数 $y = \frac{1}{2} x^{2} - 2 x - 2$ 的图象在坐标平面内绕顶点旋转180°，再向左平移3个单位，向上平移5个单位后图象对应的二次函数解析式为.

查看试题解析
16. 已知实数m，n满足m－n²＝2，则代数式m²＋2n²＋4m－1的最小值等于.

查看试题解析
17. 如图，在等边△ABC中，AC＝7，点P在△ABC内部，且∠APC＝90°，∠BPC＝120°，则△APC的面积为

查看试题解析
18. （在平面直角坐标系xOy中，抛物线y＝ax²+4ax+4a+1（a＜0）交x轴于A，B两点，若此抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）有且只有8个整点（横、纵坐标都是整数的点），则a的取值范围是.

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $2 x^{2} - 3 x - 2 = 0$ ；

(2)、 $3 x^{2} - 7 x + 3 = - 1$ .

查看试题解析
20. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4），

（ 1 ）将△ABC各顶点的横坐标保持不变，纵坐标分别减5后得到△ $A_{1} B_{1} C_{1}$ ，请在图中画出△ $A_{1} B_{1} C_{1}$ ；

（ 2 ）将△ABC绕点（1，0）按逆时针方向旋转90°后得到的△ $A_{2} B_{2} C_{2}$ ，请在图中画出△ $A_{2} B_{2} C_{2}$ ，并分别写出△ $A_{2} B_{2} C_{2}$ 的顶点坐标.

查看试题解析
21. 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．

(1)、求每个月生产成本的下降率；

(2)、请你预测4月份该公司的生产成本．

查看试题解析
22. 如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB.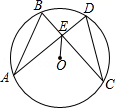

(1)、求证：AB=CD；

(2)、如果⊙O的半径为5，DE=1，求AE的长.

查看试题解析
23. 已知函数 $y = - x^{2} + (m - 1) x + m$ （m为常数）.

(1)、试说明该函数的图象与x轴始终有交点；

(2)、求证：不论m为何值，该函数的图象的顶点都在函数 $y = {(x + 1)}^{2}$ 的图象上.

(3)、当 $- 2 \leq m \leq 3$ 时，求该函数的图象的顶点纵坐标的取值范围.

查看试题解析
24. 某商家销售一款商品，进价每件80元，售价每件145元，每天销售40件，每销售一件需支付给商场管理费5元，未来一个月 $($ 按30天计算 $)$ ，这款商品将开展“每天降价1元”的促销活动，即从第一天开始每天的单价均比前一天降低1元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件，设第x天 $(1 \leq x \leq 30$ 且x为整数 $)$ 的销售量为y件．

(1)、直接写出y与x的函数关系式；

(2)、设第x天的利润为w元，试求出w与x之间的函数关系式，并求出哪一天的利润最大？最大利润是多少元？

查看试题解析
25. 如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.

(1)、求证：△AMB≌△ENB；

(2)、①当M点在何处时，AM＋CM的值最小；
②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；

(3)、当AM＋BM＋CM的最小值为 $\sqrt{3} + 1$ 时，求正方形的边长.

查看试题解析
26. 如图，在平面直角坐标系 $xOy$ 中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分C₁与经过点A、D、B的抛物线的一部分C₂组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”.已知点C的坐标为（0，），点M是抛物线C₂： $y = {mx}^{2} - 2 mx - 3 m$ （ $m$ ＜0）的顶点.

(1)、求A、B两点的坐标；

(2)、“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

(3)、当△BDM为直角三角形时，求m的值.

查看试题解析