湖北省武汉市蔡甸区2021届九年级上学期数学10月月考试卷

试卷更新日期：2020-11-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是﹣6，常数项是1的方程是（　　）

A、3x²+1＝6x B、3x²﹣1＝6x C、3x²+6x＝1 D、3x²﹣6x＝1

查看试题解析
2. 方程x²＝x的解是（　　）

A、 $x_{1} = x_{2} = 1$ B、 $x = 1$ C、 $x_{1} = 1, x_{2} = 0$ D、 $x_{1} = 1, x_{2} = - 1$

查看试题解析
3. 一元二次方程2x²﹣mx+2＝0有一根是x＝1，则另一根是（）

A、x＝1 B、x＝﹣1 C、x＝2 D、x＝4

查看试题解析
4. 二次函数y＝(x＋2)²－3的顶点坐标是（　　）

A、(2，－3) B、(－2，－3) C、(2， 3) D、(－2， 3)

查看试题解析
5. 将x²+6x+4＝0进行配方变形，下列正确的是（）

A、（x+3）²＝5 B、（x+3）²＝9 C、（x+6）²＝32 D、（x+6）²＝9

查看试题解析
6. 如果 $a < 0 ， b > 0 ， c > 0$ ，那么二次函数 $y = a x^{2} + b x + c$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
7. 若将抛物线 $y = x^{2}$ 先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（　　）

A、 $y = {(x - 1)}^{2} + 2$ B、 $y = {(x - 1)}^{2} - 2$ C、 $y = {(x + 1)}^{2} + 2$ D、 $y = {(x + 1)}^{2} - 2$

查看试题解析
8. 某种植物的主干长出若干树木的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是73，则每个支干长出（）支小分支.

A、7 B、8 C、9 D、10

查看试题解析
9. 在抛物线y= $a x^{2}$ ﹣2ax﹣3a上有A（﹣0.5， $y_{1}$ ）、B（2， $y_{2}$ ）和C（3， $y_{3}$ ）三点，若抛物线与y轴的交点在正半轴上，则 $y_{1}$ 、 $y_{2}$ 和 $y_{3}$ 的大小关系为（）

A、 $y_{3}$ ＜ $y_{1}$ ＜ $y_{2}$ B、 $y_{3}$ ＜ $y_{2}$ ＜ $y_{1}$ C、 $y_{2}$ ＜ $y_{1}$ ＜ $y_{3}$ D、 $y_{1}$ ＜ $y_{2}$ ＜ $y_{3}$

查看试题解析
10. 抛物线 $y = x^{2} + b x + 3$ 的对称轴为直线 $x = 1$ ．若关于 $x$ 的一元二次方程 $x^{2} + b x + 3 - t = 0$ （ $t$ 为实数）在 $- 1 < x < 4$ 的范围内有实数根，则 $t$ 的取值范围是（）

A、 $2 \leq t < 11$ B、 $t \geq 2$ C、 $6 < t < 11$ D、 $2 \leq t < 6$

查看试题解析

二、填空题

11. 关于x的方程(m－3)x²－x＝0是一元二次方程，则m的取值范围是.

查看试题解析
12. 一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的根的判别式是.

查看试题解析
13. 已知A（-1，3），B（2，3）是抛物线y＝ax²+bx+c（a≠0）上两点，该抛物线的对称轴是直线.

查看试题解析
14. 第七届世界军人运动会将于2019年10月18日至27日在中国武汉举行，小熙同学幸运获得了一张军运会吉祥物“兵兵”的照片，如图，该照片(中间的矩形)长29cm，宽为20cm，他想为此照片配一个四条边宽度相等的镜框(阴影部分)，且镜框所占面积为照片面积的 $\frac{1}{4}$ ，为求镜框的宽度，他设镜框的宽度为 $x$ cm，依题意列方程，化成一般式为.

查看试题解析
15. ▱ABCD中，∠B=45°，AB= $6 \sqrt{2}$ ，E为直线BC上一点，且∠CDE=15°，则DE的长为.

查看试题解析
16. 已知关于x的二次函数y＝x²－2ax＋3，当1≤x≤3时，函数有最小值2a，则a的值为.

查看试题解析
17. 如图，在宽为20m，长为32m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540m² ，则道路的宽为．

查看试题解析

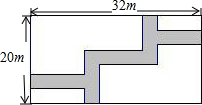
三、解答题

18. 解方程： $x^{2} - 3 x - 5 = 0$

查看试题解析
19. 如图，利用函数 $y = x^{2} - 4 x + 3$ 的图象，直接回答：

(1)、方程 $x^{2} - 4 x + 3 = 0$ 的解是；

(2)、当x时，y随x的增大而减小；

(3)、当x满足时，函数值大于0；

(4)、当 $0 < x < 5$ 时，y的取值范围是.

查看试题解析
20. 如图，在每个小正方形边长为1的网格中，点A，B，C均在格点上.

(1)、AC的长度等于；

(2)、请在图1所示的网格中，用无刻度的直尺，画出AC边上的高BH；

(3)、在图2中有一点P，若连接AP，PB，PC，满足AP平分∠A，且PC＝PB，请在如图所示的网格中，用无刻度的直尺，画出点P的位置，保留作图的痕迹.

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + (2 m + 1) x + m^{2} - 2 = 0$ .

(1)、若该方程有两个实数根，求m的取值范围；

(2)、若该方程的两个实数根为x₁ ， x₂ ，且 ${(x_{1} - x_{2})}^{2} + m^{2} = 21$ ，求m的值.

查看试题解析
22. 为满足市场需求，某超市购进一种水果，每箱进价是40元.超市规定每箱售价不得少于45元，根据以往经验发现：当售价定为每箱45元时，每天可以卖出700箱.每箱售价每提高1元，每天要少卖出20箱.

(1)、求出每天的销量y（箱）与每箱售价x（元）之间的函数关系式，并直接写出x的范围；

(2)、当每箱售价定为多少元时，每天的销售利润w（元）最大？最大利润是多少？

(3)、为稳定物价，有关部分规定：每箱售价不得高于70元.如果超市想要每天获得的利润不低于5120元，请直接写出售价x的范围.

查看试题解析
23. 已知，等边△ABC和等腰△CDE中，CD=DE，∠CDE=120°，CB=CE.

(1)、如图1，若点B和点E重合，直接写出AB与BD之间的关系；

(2)、若将如图1的△CDE绕C旋转至图2位置，连BE ，G 为BE 中点，连AG、DG，试探究AG与DG之间的关系，并证明；

(3)、如图3，∠BCE=30°，AB=6，连接BE、AD，G、H分别为BE、AD 中点，则以GH为边长的正方形的面积为(直接写出答案）.

查看试题解析
24. 如图，已知抛物线C₁的顶点为E( $\frac{1}{2} ， - \frac{9}{4}$ )，与x轴交于点A、B（点A在点B左侧），与y轴交于点C(0，－2)，

(1)、求抛物线C₁的解析式；

(2)、点D是抛物线C₁上一点，且∠ACO＋∠BCD＝45°，求点D的坐标；

(3)、M为抛物线在点B右侧上的一点，M与N两点关于抛物线的对称轴对称，MB，NA分别交y轴于P、Q两点，求OP－2OQ的值.

查看试题解析