甘肃省兰州市交通大学附属中学2021届九年级上学期数学10月月考试卷
试卷更新日期:2020-11-20 类型:月考试卷
一、单选题
-
1. 下列各组长度的线段(单位: )中,成比例线段的是( )A、1,2,3,4 B、1,2,3,6 C、2,3,4,5 D、1,3,5,102. 矩形,菱形,正方形都具有的性质是( )A、每一条对角线平分一组对角 B、对角线相等 C、对角线互相平分 D、对角线互相垂直3. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,b)对应大鱼上的点( )
 A、(-2a,2b) B、(-2a,-2b) C、(-2b,-2a) D、(-2a,-b)4. 根据下列表格的对应值:可得方程 一个解x的范围是( )
A、(-2a,2b) B、(-2a,-2b) C、(-2b,-2a) D、(-2a,-b)4. 根据下列表格的对应值:可得方程 一个解x的范围是( )0.00
0.25
0.50
0.75
1.00
1.31
3.00
A、 B、 C、 D、5. 已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )A、10 B、14 C、10或14 D、8或106. 某小组做“用频率估计概率”的实验时,绘出某一结果出现的频率折线图.如图所示,则符合这一结果的实验可能是( ) A、抛一枚硬币,出现正面朝上 B、从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球 C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃 D、掷一个正六面体的骰子,出现3点朝上7. 若分式 的值为0,则x应满足的条件是( )A、 B、 C、 D、8. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是
A、抛一枚硬币,出现正面朝上 B、从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球 C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃 D、掷一个正六面体的骰子,出现3点朝上7. 若分式 的值为0,则x应满足的条件是( )A、 B、 C、 D、8. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 A、 B、 C、5 D、69. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A、 B、 C、5 D、69. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( ) A、( ,1) B、(2,1) C、(2, ) D、(1, )10. 某商场销售一种新文具,进价为20元/件,市场调查发现,每件售价35元,每天可销售此文具250件,在此基础上,若销售单价每上涨1元,每天销售量将减少10件,针对这种文具的销售情况,若销售单价定为 元时,每天可获得4000元的销售利润,则 应满足的方程为( )A、 B、 C、 D、11. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A、( ,1) B、(2,1) C、(2, ) D、(1, )10. 某商场销售一种新文具,进价为20元/件,市场调查发现,每件售价35元,每天可销售此文具250件,在此基础上,若销售单价每上涨1元,每天销售量将减少10件,针对这种文具的销售情况,若销售单价定为 元时,每天可获得4000元的销售利润,则 应满足的方程为( )A、 B、 C、 D、11. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )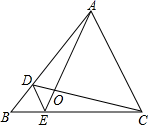 A、 B、 C、 D、12. 如图,在菱形 中,点E是 的中点,以C为圆心、 为半径作弧,交 于点F,连接 .若 , ,则阴影部分的面积为( )
A、 B、 C、 D、12. 如图,在菱形 中,点E是 的中点,以C为圆心、 为半径作弧,交 于点F,连接 .若 , ,则阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,在四边形ABCD中,对角线AC,BD交于点O,且OA=OC,OB=OD,要使四边形ABCD为矩形,则需要添加的条件是(只填一个即可).
 14. 从1,2,3,4四个数中随机选取两个不同的数,分别记为 ,则关于x的一元二次方程 有实数解的概率为.15. 如图,在 中,D、E、F分别在 、 、 上, , , , ,则 的长为.
14. 从1,2,3,4四个数中随机选取两个不同的数,分别记为 ,则关于x的一元二次方程 有实数解的概率为.15. 如图,在 中,D、E、F分别在 、 、 上, , , , ,则 的长为. 16. 若 ,且a-b+c=8,则a=.17. 如图,在 中,A,B两个顶点在x轴的上方,顶点C的坐标是 .以点C为位似中心,在x轴的下方作 的位似图形 ,并且 是把 放大到原来的2倍后得到的.设点B的对应点 的横坐标是a,则点B的横坐标是.
16. 若 ,且a-b+c=8,则a=.17. 如图,在 中,A,B两个顶点在x轴的上方,顶点C的坐标是 .以点C为位似中心,在x轴的下方作 的位似图形 ,并且 是把 放大到原来的2倍后得到的.设点B的对应点 的横坐标是a,则点B的横坐标是. 18. 如图,在 中, 于点D, 于点E, , 交于点O,F为 的中点,连接 , , ,则下列结论:① ;② ;③ ;④若 时, .其中正确的是(把所有正确结论的序号都选上)
18. 如图,在 中, 于点D, 于点E, , 交于点O,F为 的中点,连接 , , ,则下列结论:① ;② ;③ ;④若 时, .其中正确的是(把所有正确结论的序号都选上)
三、解答题
-
19. 解方程:(1)、x2-2x=4(2)、(x+1)2-3(x+1)=020. 先化简,再求值: ,其中 .21. 解方程:22. 已知关于x的一元二次方程 有两个实数根.(1)、试求k的取值范围;(2)、若此方程的两个实数根 、 ,满足 ,试求k的值.23. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
 (1)、求证:AG=CG;(2)、求证:AG2=GE·GF.24. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度.
(1)、求证:AG=CG;(2)、求证:AG2=GE·GF.24. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度. (2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?
(2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度? 25. 如图,在 中,D是 的中点,F是 边延长线上的点,连结 交 于点E.求证: .
25. 如图,在 中,D是 的中点,F是 边延长线上的点,连结 交 于点E.求证: . 26. 如图,已知矩形 , , ,P是 上一动点,M、N、E分别是 、 、 的中点.
26. 如图,已知矩形 , , ,P是 上一动点,M、N、E分别是 、 、 的中点. (1)、求证:四边形 是平行四边形;(2)、当 为何值时,四边形 是菱形,说明理由.(3)、四边形 有可能是矩形吗?若有可能,求出 的长;若不可能,请说明理由.27. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
(1)、求证:四边形 是平行四边形;(2)、当 为何值时,四边形 是菱形,说明理由.(3)、四边形 有可能是矩形吗?若有可能,求出 的长;若不可能,请说明理由.27. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类型
A
B
C
D
E
类型
新闻
体育
动画
娱乐
戏曲
人数
11
20
40
m
4
请你根据以上信息,回答下列问题:
(1)、统计表中m的值为 , 统计图中n的值为 , A类对应扇形的圆心角为度;(2)、该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;(3)、样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.28. (阅读)如图1,若 ,且点 在同一直线上,则我们把 与 称为旋转相似三角形.
 (1)、(理解)
(1)、(理解)如图2, 和 是等边三角形,点D在边 上,连接 .求证: 与 是旋转相似三角形.
 (2)、(应用)
(2)、(应用)如图3, 与 是旋转相似三角形, .求证: .
 (3)、(拓展)
(3)、(拓展)如图4, 是四边形 的对角线, , , , , .试在边 上确定一点E,使得四边形 是矩形,并说明理由.
