浙江省宁波市镇海区2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-11-20 类型:期中考试
一、选择题(每小题4分,共40分)
-
1. 抛物线y=4x2﹣3的顶点坐标是( )A、(0,3) B、(0,﹣3) C、(﹣3,0) D、(4,﹣3)2. 下列关于事件发生可能性的表述,正确的是( )A、事件:“在地面,向上抛石子后落在地上”,该事件是随机事件 B、体育彩票的中奖率为10%,则买100张彩票必有10张中奖 C、在同批次10000件产品中抽取100件发现有5件次品,则这批产品中大约有500件左 右的次品。 D、抛两枚硬币,朝上的一面是一正面一反面的概率为3. 如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( ).A、
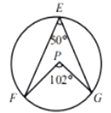 B、
B、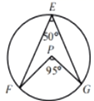 C、
C、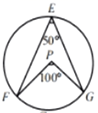 D、
D、 4. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、5. 如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,则∠PBP’的度数( )
4. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、5. 如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,则∠PBP’的度数( )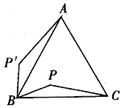 A、45° B、60° C、90° D、120°6. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、7. 圆内接四边形ABCD的四个内角之比可能是( )A、1:2:3:4 B、1:3:4:5 C、2:3:4:5 D、2:3:5:48. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)9. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
A、45° B、60° C、90° D、120°6. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、7. 圆内接四边形ABCD的四个内角之比可能是( )A、1:2:3:4 B、1:3:4:5 C、2:3:4:5 D、2:3:5:48. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)9. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )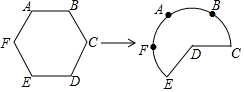 A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S210. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S210. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( ) A、4 米 B、5 米 C、2 米 D、7米
A、4 米 B、5 米 C、2 米 D、7米二、填空题(每小题5分,共30分)
-
11. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .12. 已知⊙O的半径为5,若P到圆心O的距离是4,则点P与⊙O的位置关系是 .13. 若二次函数 的图象与x轴有两个交点,则k的取值范围是.14. 一条弦所对的圆心角的度数为95°,这条弦所对的圆周角的度数为.15. 二次函数 (其中m>0),下列命题:①该函数图象过(6,0);
②该函数图象顶点在第三象限;③当x>3时,y随着x的增大而增大;④若当x<n时,都有y随着x的增大而减小,则 .正确的序号是.
16. 如图,AB为⊙O的直径,且AB=10,点C为⊙O上半圆的一点,CE⊥AB于点E,∠OCE的角平分线交⊙O于点D,弦AC=6,那么△ACD的面积是。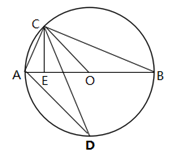
三、简答题(本大题有8小题,共80分)
-
17. 城市小区生活垃圾分为干垃圾、湿垃圾、有害垃圾和可回收垃圾四种不同的类型.(1)、甲投放了一袋垃圾,恰好是湿垃圾的概率是.(2)、甲、乙分别投放了一袋垃圾,利用树状图或列表求恰好是同一类型垃圾的概率.18. 如图,△ABC内接于⊙O,设∠B=α,请用无刻度的直尺按要求作图(保留作图痕迹).
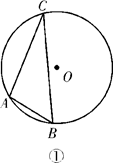
 (1)、在图①中画一个度数是2α的圆心角(2)、在图②中作出∠C的余角.19. 已知二次函数的图象经过点 和点 ,且有最小值为 .(1)、求这个函数的解析式;(2)、函数的开口方向、对称轴;(3)、当 时, 的取值范围.20. 已知:如图,在⊙O中, AB=CD , AB 与CD 相交于点 M .
(1)、在图①中画一个度数是2α的圆心角(2)、在图②中作出∠C的余角.19. 已知二次函数的图象经过点 和点 ,且有最小值为 .(1)、求这个函数的解析式;(2)、函数的开口方向、对称轴;(3)、当 时, 的取值范围.20. 已知:如图,在⊙O中, AB=CD , AB 与CD 相交于点 M .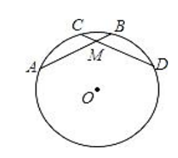
求证:
(1)、(2)、AM=DM21. 如图,A,B,C是⊙O上的点,其中 =2 ,过点B画BD⊥OC.于点D.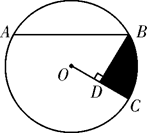 (1)、求证:AB=2BD.(2)、若AB=2 ,CD=1,求图中涂色部分的面积.22. 某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间t(天)之间的函数关系为
(1)、求证:AB=2BD.(2)、若AB=2 ,CD=1,求图中涂色部分的面积.22. 某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间t(天)之间的函数关系为p= 日销售量y(千克)与时间t(天)之间的函数关系如图所示.
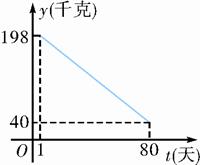 (1)、求日销售量y与时间t的函数表达式.(2)、 哪一天的日销售利润最大?最大利润是多少?23. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)、求日销售量y与时间t的函数表达式.(2)、 哪一天的日销售利润最大?最大利润是多少?23. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答: (1)、矩形奇妙四边形(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为8,∠BCD=60°.求奇妙四边形ABCD的面积;(3)、如图3,已知⊙O的内四边形ABCD是奇妙四边形,作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.24. 如图,抛物线y=- x2+ x+2与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)、矩形奇妙四边形(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为8,∠BCD=60°.求奇妙四边形ABCD的面积;(3)、如图3,已知⊙O的内四边形ABCD是奇妙四边形,作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.24. 如图,抛物线y=- x2+ x+2与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
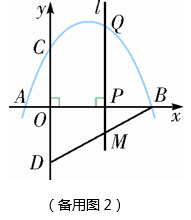 (1)、求点A,点B,点C的坐标.(2)、求直线BD的表达式.(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形.(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求点A,点B,点C的坐标.(2)、求直线BD的表达式.(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形.(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.