浙江省宁波市镇海区2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2020-11-20 类型:期中考试
一、选择题(每小题3分,共36分)
-
1. 的倒数是( ).A、 B、 C、 D、2. 下列实数中是无理数的是( ).A、 B、 C、 D、3.143. 下列各式计算结果为负数的是( ).A、 B、 C、 D、4. 近日,投资达50亿的阳明古镇一期滨水商业街正式开始营业,其中50亿用科学记数法表示为( )A、5×109 B、5×108 C、0.5×1010 D、50×1085. 64的算术平方根是( ).A、 ±4 B、4 C、±8 D、86. 与 最接近的整数是( ).A、5 B、6 C、7 D、87. 下列表述中,正确的个数是( ).
①存在绝对值最小的数;②任何数都有相反数;③绝对值等于本身的数是正数;④0是最小的有理数;⑤绝对值是同一个正数的数有两个,它们互为相反数.
A、1个 B、2个 C、3个 D、4个8. 若a2=9,b2=4,且ab<0,则a−b的值为( ).A、5 B、−2 C、±5 D、±29. 以下说法,正确的是( ).A、数据475301精确到万位可表示为480000. B、王平和李明测量同一根钢管的长,按四舍五入法得到结果分别是0.80米和0.8米,这两个结果是相同的. C、近似数1.5046精确到0.01,结果可表示为1.50. D、小林称得体重为42千克,其中的数据是准确数.10. 如图,面积为3的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( ).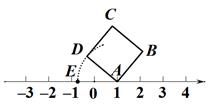 A、− B、1− C、−1− D、11. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.
A、− B、1− C、−1− D、11. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.①
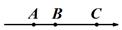 ②
② 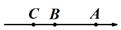 ③
③ 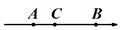 ④
④ 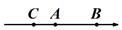 A、1个 B、2个 C、3个 D、4个12. 将正偶数按照如下规律进行分组排列,依次为(2),(4,6),(8,10,12),(14,16,18,20)…,我们称“4”是第2组第1个数字,“16”是第4组第2个数字,若2020是第m组第n个数字,则m+n=( ).A、64 B、65 C、66 D、67
A、1个 B、2个 C、3个 D、4个12. 将正偶数按照如下规律进行分组排列,依次为(2),(4,6),(8,10,12),(14,16,18,20)…,我们称“4”是第2组第1个数字,“16”是第4组第2个数字,若2020是第m组第n个数字,则m+n=( ).A、64 B、65 C、66 D、67二、填空题(每小题3分,共18分)
-
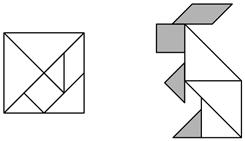
13. 的相反数是.14. 如果收入100元记作+100元,则支出50元记作元.15. 若规定一种运算:a*b=a−b+ab,则3*(−2)=.16. 某粮店出售的两种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg的字样,从中任意拿出两袋,它们的质量最多相差kg.17. 1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即: 如果正整数m最少经过6步运算可得到1,则m的值为.18. 七巧板被西方人称为“东方魔术”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图1)边长为a(cm).若图2的“小兔子”图案中的阴影部分面积为12cm2 , 那么a=cm.
三、解答题(共66分)
-
19. 把下列各数之前的序号填在相应的大括号内:
① ,②−0.31,③−(−2),④ ,⑤ ,⑥0,⑦ ,⑧1.1010010001…(每两个1之间依次多一个0),⑨1.732
(1)、正分数集合:{}(2)、负有理数集合:{}(3)、无理数集合:{}(4)、非负整数集合:{}20. 计算:(1)、3×2−(−8)÷2(2)、(3)、21. 把下列实数表示在数轴上,并比较它们的大小(用“<”连接).(−2)2 , ,0,−1,
 22.(1)、如果|m−4|+(n+5)2=0,求(m+n)2021+m3的值;(2)、已知实数a,b,c,d,e,且a,b互为倒数,c,d互为相反数,e的绝对值为2,求 的值.23. 在学习《实数》内容时,我们通过“逐步逼近”的方法可以计算出 的近似值,得出1.4< <1.5.利用“逐步逼近“法,请回答下列问题:(1)、 介于连续的两个整数a和b之间,且a<b,那么a= , b=.(2)、x是 +2的小数部分,y是 −1的整数部分,则x= , y=.(3)、在(2)的条件下,求( −x)y的平方根.24. 有8筐杨梅,以每筐5千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下(单位:kg):
22.(1)、如果|m−4|+(n+5)2=0,求(m+n)2021+m3的值;(2)、已知实数a,b,c,d,e,且a,b互为倒数,c,d互为相反数,e的绝对值为2,求 的值.23. 在学习《实数》内容时,我们通过“逐步逼近”的方法可以计算出 的近似值,得出1.4< <1.5.利用“逐步逼近“法,请回答下列问题:(1)、 介于连续的两个整数a和b之间,且a<b,那么a= , b=.(2)、x是 +2的小数部分,y是 −1的整数部分,则x= , y=.(3)、在(2)的条件下,求( −x)y的平方根.24. 有8筐杨梅,以每筐5千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下(单位:kg):
回答下列问题:
(1)、这8筐杨梅中,最接近5千克的那筐杨梅为多少千克?(2)、以每筐5千克为标准,这8筐杨梅总计超过多少千克或者不足多少千克?(3)、若杨梅每千克售价40元,则出售这8筐杨梅可卖多少元?25. 有依次排列的3个数:6,8,3,对任意相邻的两个数,都用左边的数减去右边的数,所得之差写在两个数之间,可产生一个新数串①:6,−2,8,5,3,这称作第一次操作;对数串①进行同样的操作后也可产生一个新的数串②:6,8,−2,−10,8,3,5,2,3……依次操作下去.(1)、数串①的所有数之和为 , 数串②的所有数之和为.(2)、第3次操作以后所产生的数串③为6, , 8,10,−2,8,−10,−18,8,5,3,-2,5,3,2,−1,3.所有数之和为.(3)、请列式计算:操作第2020次产生的新数串的所有数字之和是多少?