浙江省宁波市镇海区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-11-20 类型:期中考试
一、选择题(每小题3分,共36分)
-
1. 下列防疫图标中的图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 三角形的两边长分别是5和7,则第三边长不可能是( )A、6 B、8 C、9 D、123. 若 ,运用不等式的性质,下列各式中变形一定成立的是( )A、 B、 C、 D、4. 直角三角形两条直角边长分别是5和12,则第三边上的中线长为( )A、6 B、6.5 C、8 D、105. 已知等腰三角形的一个角是100°,则它的底角是( )A、40° B、60° C、80° D、40°或100°6. 下列问题的解答正确的是( )A、m的3倍不大于n的 , 可表示为3m< B、 ≥0 C、a是非负数,可表示为a>0 D、7. 如图,在△ABC中,AD⊥BC , AE平分∠BAC , 若∠BAE=30°,∠CAD=20°,则∠B=( )
2. 三角形的两边长分别是5和7,则第三边长不可能是( )A、6 B、8 C、9 D、123. 若 ,运用不等式的性质,下列各式中变形一定成立的是( )A、 B、 C、 D、4. 直角三角形两条直角边长分别是5和12,则第三边上的中线长为( )A、6 B、6.5 C、8 D、105. 已知等腰三角形的一个角是100°,则它的底角是( )A、40° B、60° C、80° D、40°或100°6. 下列问题的解答正确的是( )A、m的3倍不大于n的 , 可表示为3m< B、 ≥0 C、a是非负数,可表示为a>0 D、7. 如图,在△ABC中,AD⊥BC , AE平分∠BAC , 若∠BAE=30°,∠CAD=20°,则∠B=( ) A、45° B、60° C、50° D、55°8. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形 C、两个全等的三角形面积相等 D、直角三角形斜边上的中线等于斜边的一半9. 若△ABC三边长a,b,c满足|a2-b2|+(c-a)2=0,则△ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形10. 如图,所示的正方形网格中,网格线的交点称为格点.已知A、B两点为格点,如果C也是图中的格点,则满足△ABC为等腰三角形的点C的个数为( )
A、45° B、60° C、50° D、55°8. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形 C、两个全等的三角形面积相等 D、直角三角形斜边上的中线等于斜边的一半9. 若△ABC三边长a,b,c满足|a2-b2|+(c-a)2=0,则△ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形10. 如图,所示的正方形网格中,网格线的交点称为格点.已知A、B两点为格点,如果C也是图中的格点,则满足△ABC为等腰三角形的点C的个数为( )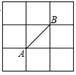 A、6个 B、7个 C、8个 D、9个11. 如图,在已知的△ABC中,按以下步骤作图:
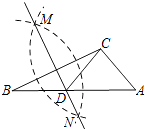
A、6个 B、7个 C、8个 D、9个11. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为( )
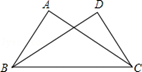
 A、90° B、95° C、100° D、105°12. 如图,D,E分别是△ABC的边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1 , △CEF的面积为S2 , 若S△ABC=12,则S1﹣S2=( )
A、90° B、95° C、100° D、105°12. 如图,D,E分别是△ABC的边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1 , △CEF的面积为S2 , 若S△ABC=12,则S1﹣S2=( ) A、1.5 B、2 C、3 D、0.5
A、1.5 B、2 C、3 D、0.5二、填空题 (每小题3分,共18分)
-
13. 在△ABC中,∠C=90°,∠A:∠B=1: 2,则∠B=.14. 把命题:“内错角相等”改写成“如果......那么......”的形式是.15. 如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是(填一个即可).
 16. 若x>y,且(m-5)x <(m-5)y ,则m的取值范围是.17. 一个等腰三角形的底边长为5,一条腰上的中线把周长分成的两部分的差为2,则这个等腰三角形的腰长为.18. 如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为.
16. 若x>y,且(m-5)x <(m-5)y ,则m的取值范围是.17. 一个等腰三角形的底边长为5,一条腰上的中线把周长分成的两部分的差为2,则这个等腰三角形的腰长为.18. 如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为.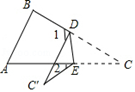
三、解答题(第
-
19. 在不同的数轴上表示下列不等式,并分别写出满足不等式的所有负整数。(1)、x> 2
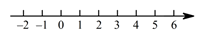 (2)、-2≤x<1
(2)、-2≤x<1 20. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形:
20. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形: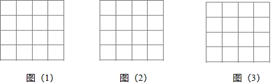 (1)、在图(1)中,画一个直角三角形,使它的三边长都是有理数;(2)、在图(2)中,画一个等腰直角三角形,使它的三边长都是无理数;(3)、在图(3)中,画一个正方形,使它的面积是8.21. 某数学兴趣小组在学习“不等式的性质”时,有两名同学的对话如下:
(1)、在图(1)中,画一个直角三角形,使它的三边长都是有理数;(2)、在图(2)中,画一个等腰直角三角形,使它的三边长都是无理数;(3)、在图(3)中,画一个正方形,使它的面积是8.21. 某数学兴趣小组在学习“不等式的性质”时,有两名同学的对话如下: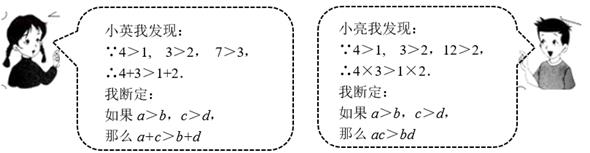
你认为小英和小亮的结论正确吗?如果正确,请说明理由;如果不正确,请举出一个反例。
22. 如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.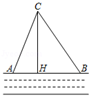 (1)、问CH是否为从村庄C到河边的最近路?请通过计算加以说明;(2)、求新路CH比原路CA少多少千米?23. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
(1)、问CH是否为从村庄C到河边的最近路?请通过计算加以说明;(2)、求新路CH比原路CA少多少千米?23. 如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,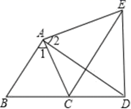 (1)、试说明△ABD与△ACE全等的理由;(2)、如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.24. 某水果批发站购进苹果和梨共100箱,其中苹果每箱40元,梨每箱45元。(1)、若设苹果箱数为x箱,总费用为y元,试用x的代数式来表示总费用y.(2)、若购进的100箱水果中,苹果箱数不小于30箱,且不大于90箱,试求该水果批发站此次购入水果的总费用的范围.25. 定义:线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
(1)、试说明△ABD与△ACE全等的理由;(2)、如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.24. 某水果批发站购进苹果和梨共100箱,其中苹果每箱40元,梨每箱45元。(1)、若设苹果箱数为x箱,总费用为y元,试用x的代数式来表示总费用y.(2)、若购进的100箱水果中,苹果箱数不小于30箱,且不大于90箱,试求该水果批发站此次购入水果的总费用的范围.25. 定义:线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题: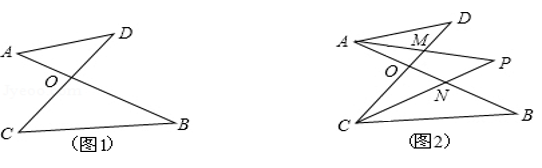 (1)、在图1中,∠A、∠B、∠C、∠D之间的关系为.(2)、如图2,在(1)的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.
(1)、在图1中,∠A、∠B、∠C、∠D之间的关系为.(2)、如图2,在(1)的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.①仔细观察,在图2中有 ▲ 个以线段AD为边的“8字形”;
②若∠D=40°,∠B=36°,试求∠P的度数(请说明理由);
③∠D和∠B为任意角时,其他条件不变,试直接写出∠P与∠D、∠B之间的数量关系,不需说明理由.
26. 阅读下列材料,解决提出的问题: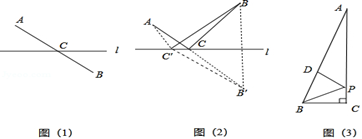
【最短路径问题】
如图(1),点A,B分别是直线l异侧的两个点,如何在直线l上找到一个点C,使得点C到点A,点B的距离和最短?我们只需连接AB,与直线l相交于一点,可知这个交点即为所求.
如图(2),如果点A,B分别是直线l同侧的两个点,如何在l上找到一个点C,使得这个点到点A、点B的距离和最短?我们可以利用轴对称的性质,作出点B关于的对称点B’,这时对于直线l上的任一点C,都保持CB=CB’,从而把问题(2)变为问题(1).因此,线段AB’与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求,我们不妨在直线上另外任取一点C’,连接AC’,BC’,B’C’.
因为AB’≤AC’+C’B’ , ∴AC+CB≤AC’+C’B,即AC+BC最小.
(1)、【数学思考】材料中划线部分的依据是.
(2)、材料中解决图(2)所示问题体现的数学思想是 .(填字母代号即可)A、转化思想 B、分类讨论思想 C、整体思想(3)、【迁移应用】如图3,在Rt△ABC中,∠C=90°,∠BAC=15°,点P为C边上的动点,点D为AB边上的动点,若AB=6cm,求BP+DP的最小值.