浙江省宁波市鄞州区七校联考2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-11-20 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列长度的三条线段,能组成三角形的是( )A、3,5,7 B、3,6,10 C、5,5,11 D、5,6,112. 下列图标中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知实数a,b,若a>b,则下列结论错误的是( )A、a-7>b-7 B、6+a>b+6 C、 D、-3a>-3b4. 下列四个选项中,属于命题的是( )A、两点能确定一条直线吗 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、∠A的平分线AM5. 一个等腰三角形的顶角是50°,则它的底角是()A、100° B、65° C、70° D、75°6. 如图,在△ABC中,AB边上的高为( )
3. 已知实数a,b,若a>b,则下列结论错误的是( )A、a-7>b-7 B、6+a>b+6 C、 D、-3a>-3b4. 下列四个选项中,属于命题的是( )A、两点能确定一条直线吗 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、∠A的平分线AM5. 一个等腰三角形的顶角是50°,则它的底角是()A、100° B、65° C、70° D、75°6. 如图,在△ABC中,AB边上的高为( )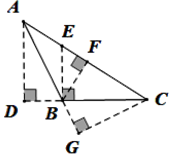 A、CG B、BF C、BE D、AD7. 如图,将一副三角板重叠放在起,使直角顶点重合于点O.若 ,则 ( )
A、CG B、BF C、BE D、AD7. 如图,将一副三角板重叠放在起,使直角顶点重合于点O.若 ,则 ( )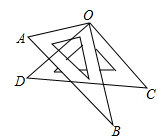 A、 B、 C、 D、8. 满足下列条件的是直角三角形的是( )A、 , , B、 , , C、 D、9. 如图, 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以D,E为圆心、以大于 为长的半径作弧,两弧在 内交于点F;作射线 交 于点G,若 ,P为 上一动点,则 的最小值为( )
A、 B、 C、 D、8. 满足下列条件的是直角三角形的是( )A、 , , B、 , , C、 D、9. 如图, 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以D,E为圆心、以大于 为长的半径作弧,两弧在 内交于点F;作射线 交 于点G,若 ,P为 上一动点,则 的最小值为( )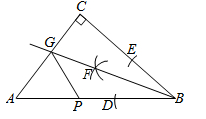 A、无法确定 B、 C、1 D、210. 如图,△ABC中,AC=BC=1,∠ACB=90°,以AC、BC、AB为边作如图所示的等边△ABD,等边△ACE,等边△BCF,连结DE,DF,则四边形DFCE的面积为( )
A、无法确定 B、 C、1 D、210. 如图,△ABC中,AC=BC=1,∠ACB=90°,以AC、BC、AB为边作如图所示的等边△ABD,等边△ACE,等边△BCF,连结DE,DF,则四边形DFCE的面积为( )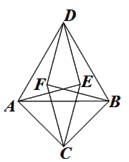 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题(每小题3分,共18分)
-
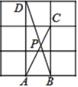
11. 在△ABC中,已知∠A=∠B=2∠C,则∠C=.12. 不等式 的最大整数解是.13. 已知一个直角三角形的两边长分别为4和3,则它的斜边长为.14. 等腰三角形一腰上的中线将这个三角形的周长分成21,12两部分,则等腰三角形的腰长为.15. 如图,在 的网格中,每一个小正方形的边长都是1,点 、 、 、 都在格点上,连接 , 相交于 ,那么 的大小是.
 16. 如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为.
16. 如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为.
三、解答题(第17~18题每题5分,第19~22每题6分,第23题8分,第24题10分,共52分)
-
17. 解不等式:3x-1≥2(x-1),并把它的解集在数轴上表示出来.
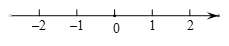 18. 如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.
18. 如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.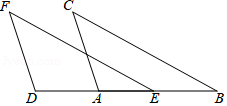 19. 如图,在2×2的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中△ABC是一个格点三角形.请在下面每一个图中,作出一个与△ABC成轴对称的格点三角形.(画三个,不能重复)
19. 如图,在2×2的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中△ABC是一个格点三角形.请在下面每一个图中,作出一个与△ABC成轴对称的格点三角形.(画三个,不能重复) 20. 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连结EF,CF.
20. 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连结EF,CF.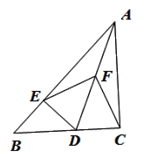 (1)、若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.(2)、在(1)的条件下,若∠BAC=45°,AD=6,求C、E两点间的距离.21. 已知:如图,在△ABC中,AB=BC,∠ABC=90°,点E在BC上,点F在AB的延长线上,且AE=CF .
(1)、若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.(2)、在(1)的条件下,若∠BAC=45°,AD=6,求C、E两点间的距离.21. 已知:如图,在△ABC中,AB=BC,∠ABC=90°,点E在BC上,点F在AB的延长线上,且AE=CF . (1)、求证:△ABE ≌ △CBF.(2)、若∠ACF=70°,求∠EAC的度数.22. 某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)、求证:△ABE ≌ △CBF.(2)、若∠ACF=70°,求∠EAC的度数.22. 某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)、求修建一个足球场和一个篮球场各需多少万元?(2)、该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
23. 已知△ABC,点P为其内部一点,连结PA、PB、PC,在△PAB,△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.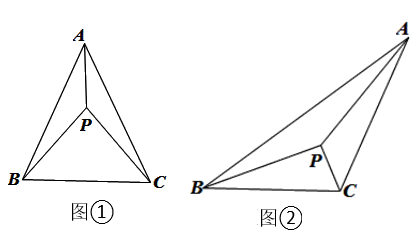 (1)、判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”.
(1)、判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”.①内角分别为30°、60°、90°的三角形存在等角点;命题;
②任意的三角形都存在等角点;命题.
(2)、如图 ①,点P是△ABC的等角点,若∠BAC=∠PBC,探究图 ①中∠BPC,∠ABC,∠ACP之间的数量关系,并说明理由;(3)、如图②,在△ABC中,∠BAC<∠ABC<∠ACB,若△ABC的三个内角的角平分线的交点P是该三角形的等角点,直接写出△ABC三个内角的度数.24. 如图①,点P、Q 分别是等边△ABC边AB、BC上的动点(端点除外),点 P从顶点 A、点Q从顶点B 同时出发,且它们的运动速度相同,连接AQ、CP交于点M.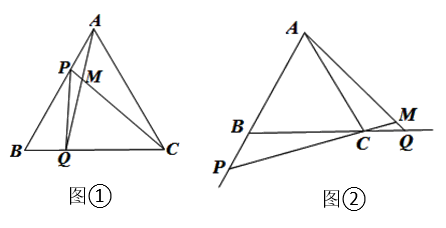 (1)、求证:△ABQ≌△CAP;(2)、当点P、Q 分别在 AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图②,若点 P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,求∠QMC的度数.
(1)、求证:△ABQ≌△CAP;(2)、当点P、Q 分别在 AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图②,若点 P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,求∠QMC的度数.