河南省信阳市冯店一中2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-11-20 类型：期中考试

进入出卷网下载

一、单选题

1. 若关于x的一元二次方程x²﹣2x+m=0有一个解为x=﹣1，则另一个解为（）

A、1 B、﹣3 C、3 D、4

查看试题解析
2. 下列一元二次方程中，没有实数根的是（）.

A、 $x^{2} - 2 x = 0$ B、 $x^{2} + 4 x - 1 = 0$ C、 $3 x^{2} - 5 x + 2 = 0$ D、 $2 x^{2} - 4 x + 3 = 0$

查看试题解析
3. 一元二次方程x²－2x＋b＝0的两根分别为x₁和x₂ ，则x₁＋x₂为（）

A、－2 B、b C、2 D、－b

查看试题解析
4. 已知二次函数y=x²﹣x+ $\frac{1}{4}$ m﹣1的图象与x轴有交点，则m的取值范围是（）

A、m≤5 B、m≥2 C、m＜5 D、m＞2

查看试题解析
5. 某品牌手机三月份销售400万部，四月份、五月份销售量连续增长，五月份销售量达到900万部，求月平均增长率．设月平均增长率为 $x$ ，根据题意列方程为（）．

A、 $400 (1 + x^{2}) = 900$ B、 $400 (1 + 2 x) = 900$ C、 $900 {(1 ﹣ x)}^{2} = 400$ D、 $400 {(1 + x)}^{2} = 900$

查看试题解析
6. 抛物线 $y = x^{2} + 6 x + 7$ 可由抛物线 $y = x^{2}$ 如何平移得到的（）

A、先向左平移3个单位，再向下平移2个单位 B、先向左平移6个单位，再向上平移7个单位 C、先向上平移2个单位，再向左平移3个单位 D、先回右平移3个单位，再向上平移2个单位

查看试题解析
7. 若二次函数y=|a|x²+bx+c的图象经过A(m ， n)、B(0，y₁)、C(3－m ， n)、D( $\sqrt{2}$ ， y₂)、E(2，y₃)，则y₁、y₂、y₃的大小关系是（）.

A、y₁< y₂< y₃ B、y₁ < y₃< y₂ C、y₃< y₂< y₁ D、y₂< y₃< y₁

查看试题解析
8. 某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（）

A、 $2500 {(1 + x)}^{2} ＝ 9100$ B、 $2500 {(1 + x %)}^{2} ＝ 9100$ C、 $2500 (1 + x) + 2500 {(1 + x)}^{2} ＝ 9100$ D、 $2500 + 2500 (1 + x) + 2500 {(1 + x)}^{2} ＝ 9100$

查看试题解析
9. 已知 $a ， b$ 是非零实数， $| a | > | b |$ ，在同一平面直角坐标系中，二次函数 $y_{1} = a x^{2} + b x$ 与一次函数 $y_{2} = a x + b$ 的大致图象不可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴交于点 $(- 3 ， 0)$ ，其对称轴为直线 $x = - \frac{1}{2}$ ，结合图象分析下列结论：① $a b c > 0$ ；② $3 a + c > 0$ ；③当 $x < 0$ 时， $y$ 随 $x$ 的增大而增大；④一元二次方程 $c x^{2} + b x + a = 0$ 的两根分别为 $x_{1} = - \frac{1}{3}$ ， $x_{2} = \frac{1}{2}$ ；⑤ $\frac{b^{2} - 4 a c}{4 a} < 0$ ；⑥若 $m$ ， $n (m < n)$ 为方程 $a (x + 3) (x ﹣ 2) + 3 = 0$ 的两个根，则 $m < - 3$ 且 $n > 2$ ，其中正确的结论有（）

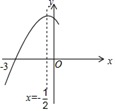A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 已知x= $2 + \sqrt{3}$ 是关于x的方程 $x^{2} - 4 x + m = 0$ 的一个根，则m＝.

查看试题解析
12. 将二次函数 $y = x^{2} - 4 x + 5$ 化成 $y = a {(x - h)}^{2} + k$ 的形式为.

查看试题解析
13. 一元二次方程 $3 x^{2} = 4 - 2 x$ 的解是．

查看试题解析
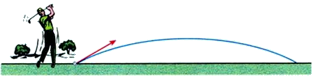
14. 如图，若被击打的小球飞行高度 $h$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）之间具有的关系为 $h = 20 t - 5 t^{2}$ ，则小球从飞出到落地所用的时间为 $s$ .

查看试题解析
15.
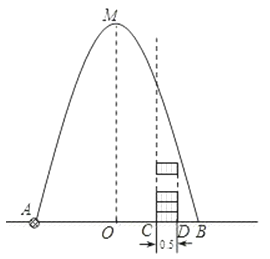
如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B，有人在直线AB上点C（靠点B一侧）竖直向上摆放若干个无盖的圆柱形桶．试图让网球落入桶内，已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．当竖直摆放圆柱形桶至少个时，网球可以落入桶内．

查看试题解析

三、解答题

16. 用适当的方法解方程：

(1)、x²－4x＋2＝0；

(2)、(2x－1)²＝x(3x＋2)－7.

查看试题解析
17. 如图，已知抛物线y₁＝－2x²＋2与直线y₂＝2x＋2交于A，B两点.

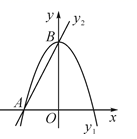(1)、求A，B两点的坐标；

(2)、若y₁＞y₂ ，请直接写出x的取值范围.

查看试题解析
18. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析
19. 已知抛物线y=ax²+bx+c与x轴交于点A（1，0），B（3，0），且过点C（0，﹣3）．

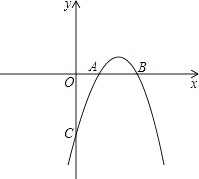(1)、求抛物线的解析式和顶点坐标；

(2)、请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=﹣x上，并写出平移后抛物线的解析式．

查看试题解析
20. 2016年，某贫困户的家庭年人均纯收入为2500元，通过政府产业扶持，发展了养殖业后，到2018年，家庭年人均纯收入达到了3600元.

(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率；

(2)、若年平均增长率保持不变，2019年该贫困户的家庭年人均纯收入是否能达到4200元？

查看试题解析
21. 如图，抛物线y＝(x－1)²＋k与x轴相交于A，B两点(点A在点B的左侧)，与y轴相交于点C(0，－3)，P为抛物线上一点，横坐标为m，且m＞0.

(1)、求此抛物线的解析式；

(2)、当点P位于x轴下方时，求△ABP面积的最大值；

(3)、设此抛物线在点C与点P之间部分(含点C和点P)最高点与最低点的纵坐标之差为h.
①求h关于m的函数解析式，并写出自变量m的取值范围；

②当h＝9时，直接写出△BCP的面积.

查看试题解析
22. 为迎接“世界华人炎帝故里寻根节”，某工厂接到一批纪念品生产订单，按要求在15天内完成，约定这批纪念品的出厂价为每件20元，设第x天（1≤x≤15，且x为整数）每件产品的成本是p元，p与x之间符合一次函数关系，部分数据如表：
天数（x）
1
3
6
10
每件成本p（元）
7.5
8.5
10
12
任务完成后，统计发现工人李师傅第x天生产的产品件数y（件）与x（天）满足如下关系：y= ${\begin{matrix} 2 x + 20 (1 \leq x < 10 ，且 x 为整数) \\ 40 (10 \leq x \leq 15 ，且 x 为整数) \end{matrix}$ ，
设李师傅第x天创造的产品利润为W元．

(1)、直接写出p与x，W与x之间的函数关系式，并注明自变量x的取值范围：

(2)、求李师傅第几天创造的利润最大？最大利润是多少元？

(3)、任务完成后．统计发现平均每个工人每天创造的利润为299元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金．请计算李师傅共可获得多少元奖金？

查看试题解析
23. 如图，在平面直角坐标系中，Rt△ABC的边BC在x轴上，∠ABC＝90°，以A为顶点的抛物线y＝－x²＋bx＋c经过点C(3，0)，交y轴于点E(0，3)，动点P在对称轴上.

(1)、求抛物线解析式；

(2)、若点P从A点出发，沿A→B方向以1个单位/秒的速度匀速运动到点B停止，设运动时间为t秒，过点P作PD⊥AB交AC于点D，过点D平行于y轴的直线l交抛物线于点Q，连接AQ，CQ，当t为何值时，△ACQ的面积最大？最大值是多少？

(3)、若点M是平面内的任意一点，在x轴上方是否存在点P，使得以点P，M，E，C为顶点的四边形是菱形，若存在，请直接写出符合条件的M点坐标；若不存在，请说明理由.

查看试题解析

天数（x）	1	3	6	10
每件成本p（元）	7.5	8.5	10	12