重庆市西北狼教育联盟2020-2021学年八年级上学期数学开学试卷
试卷更新日期:2020-11-20 类型:开学考试
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 下列方程是一元一次方程的是( )A、x2﹣2x=0 B、2x﹣5y=4 C、x+2=0 D、3. 如果 与 是同类项,则x、y的值分别是( )A、 B、 C、 D、4. 不等式 的解集在数轴上表示正确的是( )A、
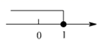 B、
B、 C、
C、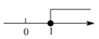 D、
D、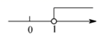 5. 2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线, 不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体 中,与汉字“抗”相对的面上的汉字是( )
5. 2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线, 不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体 中,与汉字“抗”相对的面上的汉字是( )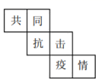 A、 共 B、同 C、疫 D、情6. 下列说法中正确的有( )
A、 共 B、同 C、疫 D、情6. 下列说法中正确的有( )①在同一平面内,不重合的两条直线若不相交,则必平行;②在同一平面内,不相交的两条线段必平行;③相等的角是对顶角;④两条直线被第三条直线所截,所得的同位角相等;⑤两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
A、1个 B、2个 C、3个 D、4个7. 将一个长方形纸片 如图所示折叠, ,则 为( )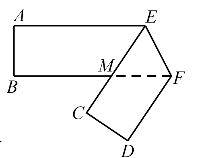 A、 B、 C、 D、8. 我国古代数学名著《九章算术》中记载有这样一道题:“今有二马、一牛价过一万,如半马之价;一马二牛价不满一万,如半牛之价.1问牛、马价各几何?”其大意是:今有2匹马、1头牛的总价超过10000钱,其超出的钱数相当于 匹马的价格;1匹马、2头牛的总价不足1000钱,所差的钱数相当于 头牛的价格.问每头牛、每匹马的价格各是多少?若设每头牛的价格为x钱,每匹马的价格为y钱,则根据题意列方程组正确的为 ( )A、 B、 C、 D、9. 如图,在 中, 是高, 是两内角平分线,它们相交于点 , , ,求 和 的度数之和为( )
A、 B、 C、 D、8. 我国古代数学名著《九章算术》中记载有这样一道题:“今有二马、一牛价过一万,如半马之价;一马二牛价不满一万,如半牛之价.1问牛、马价各几何?”其大意是:今有2匹马、1头牛的总价超过10000钱,其超出的钱数相当于 匹马的价格;1匹马、2头牛的总价不足1000钱,所差的钱数相当于 头牛的价格.问每头牛、每匹马的价格各是多少?若设每头牛的价格为x钱,每匹马的价格为y钱,则根据题意列方程组正确的为 ( )A、 B、 C、 D、9. 如图,在 中, 是高, 是两内角平分线,它们相交于点 , , ,求 和 的度数之和为( ) A、 B、 C、 D、10. 上图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )
A、 B、 C、 D、10. 上图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( ) A、88 B、89 C、90 D、9111. 甲、乙两人分别从 两地同时骑自行车相向而行,2小时后在途中相遇,相遇后,甲、乙骑自行车的速度都提高了1千米/小时,当甲到达地后立刻以原路和提高后的速度向地返行,乙到达 地后也立刻以原路和提高后的速度向 地返行.甲、乙两人在开始 出发后的5小时36分钟又再次相遇,则 两地的距离是( )A、24千米 B、30千米 C、32千米 D、36千米12. 如图,直线 ,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连结NE、NM,过点N作NG平分 交直线CD于点G,过点N作 ,交直线CD于点F,若 ,则 的度数为( )
A、88 B、89 C、90 D、9111. 甲、乙两人分别从 两地同时骑自行车相向而行,2小时后在途中相遇,相遇后,甲、乙骑自行车的速度都提高了1千米/小时,当甲到达地后立刻以原路和提高后的速度向地返行,乙到达 地后也立刻以原路和提高后的速度向 地返行.甲、乙两人在开始 出发后的5小时36分钟又再次相遇,则 两地的距离是( )A、24千米 B、30千米 C、32千米 D、36千米12. 如图,直线 ,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连结NE、NM,过点N作NG平分 交直线CD于点G,过点N作 ,交直线CD于点F,若 ,则 的度数为( )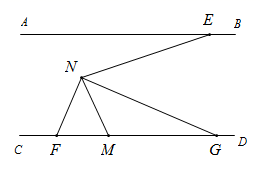 A、110° B、115° C、120° D、125°
A、110° B、115° C、120° D、125°二、填空题
-
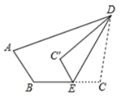
13. “a的一半与1的差不大于5”用不等式表示为.14. 如图,在四边形中, , 与 互为补角,点 在 上,将 沿 翻折,得到 ,若 , 平分 ,则 的度数为 ;
 15. 若不等式组 有解,则a的取值范围是.16. 如图,将直角三角形 沿着点 到 的方向平移到三角形 的位置, , ,平移的距离为6,则阴影部分的面积为.
15. 若不等式组 有解,则a的取值范围是.16. 如图,将直角三角形 沿着点 到 的方向平移到三角形 的位置, , ,平移的距离为6,则阴影部分的面积为.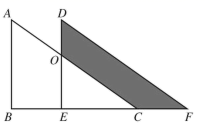 17. 已知关于 的二元一次方程组 的解满足 ,且关于 的不等式组 无解,那么所有符合条件的整数 的个数为.18. 随着新冠肺炎疫情逐步得到控制,全国各地各类学校逐渐实行复学.我校为了保证师生能够顺利的复学以及返校后师生的身体健康,早在3月份学校两次同时购进了医用口罩、消毒液两种防疫医用产品,第一次购进医用口罩的包数比消毒液的瓶数多 ,第二次购进医用口罩的包数比第一次购进的医用口罩的数量少 ,结果第二次购买两种医用产品的总数量比第一次购买两种医用产品的总数量多 ,第二次购买的医用口罩、消毒液两种医用产品的总费用比第一次购买的医用口罩、消毒液两种医用产品的总费用少 (假设医用口罩、消毒液两种医用产品的单价不变),则消毒液与医用口罩的单价的比值是.19. 完成下面的证明过程:
17. 已知关于 的二元一次方程组 的解满足 ,且关于 的不等式组 无解,那么所有符合条件的整数 的个数为.18. 随着新冠肺炎疫情逐步得到控制,全国各地各类学校逐渐实行复学.我校为了保证师生能够顺利的复学以及返校后师生的身体健康,早在3月份学校两次同时购进了医用口罩、消毒液两种防疫医用产品,第一次购进医用口罩的包数比消毒液的瓶数多 ,第二次购进医用口罩的包数比第一次购进的医用口罩的数量少 ,结果第二次购买两种医用产品的总数量比第一次购买两种医用产品的总数量多 ,第二次购买的医用口罩、消毒液两种医用产品的总费用比第一次购买的医用口罩、消毒液两种医用产品的总费用少 (假设医用口罩、消毒液两种医用产品的单价不变),则消毒液与医用口罩的单价的比值是.19. 完成下面的证明过程: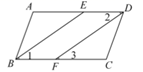
如图, , 平分 , 平分 .
求证: .
证明: ,(已知)
(_▲__)
又 ,(已知)
_▲_
(_▲__)
平分 ,(已知)
.同理,
(已知)
(_▲_)
(_▲__)
三、解答题
-
20.(1)、解方程组(2)、解不等式21. 一个两位数,十位数字是个位数字的两倍,将这个两位数的十位数字与个位数字对调后得到的两位数比原来的两位数小27,求这个两位数.22. 已知方程组 的解满足x为非正数,y为负数.(1)、求m的取值范围;(2)、在(1)的条件下,若不等式 的解为 ,请写出整数m的值.23. 为应对新冠肺炎疫情,某服装厂决定转型生产口罩,根据现有厂房大小决定购买10条口罩上产线,现有甲、乙两种型号的口罩生产线可供选择.经调查:购买3台甲型口罩生产线比购买2台乙型口罩生产线多花14万元,购买4条甲型口罩生产线与购买5条乙型口罩生产线所需款数相同.(1)、求甲、乙两种型号口罩生产线的单价;(2)、已知甲型口罩生产线每天可生产口罩9万只,乙型口罩生产线每年可生产口罩7万只,若每天要求产量不低于75万只,预算购买口罩生产线的资金不超过90万元,该厂有哪几种购买方案?哪种方案最省钱?最少费用是多少?24. 如图,四边形 ABCD 中,AE,DF 分别是∠BAD,∠ADC 的平分线,且 AE⊥DF 于点 O . 延长 DF 交 AB 的延长线于点 M .
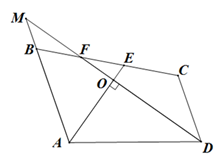 (1)、求证:AB∥DC ;(2)、若∠MBC=120°,∠BAD=108°,求∠C,∠DFE 的度数.
(1)、求证:AB∥DC ;(2)、若∠MBC=120°,∠BAD=108°,求∠C,∠DFE 的度数.