陕西省渭南市富平县2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-11-20 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中.点P（1，﹣2）关于x轴的对称点的坐标是（）

A、（1，2） B、（﹣1，﹣2） C、（﹣1，2） D、（﹣2，1）

查看试题解析
2. 要使二次根式 $\sqrt{1 - 2 x}$ 有意义，字母的取值范围是（）

A、x≥ $\frac{1}{2}$ B、x≤ $\frac{1}{2}$ C、x＞ $\frac{1}{2}$ D、x＜ $\frac{1}{2}$

查看试题解析
3. 在某市举办的垂钓比赛上，5名垂钓爱好者参加了比赛，比赛结束后，统计了他们各自的钓鱼条数，成绩如下：4，5，10，6，10．则这组数据的中位数是（　　）

A、5 B、6 C、7 D、10

查看试题解析
4. 如果 ${\begin{cases} x = - 3 \\ y = 1 \end{cases}$ 是方程ax＋(a－2)y＝0的一组解，则a的值是（）

A、1 B、－1 C、2 D、－2

查看试题解析
5. 如图，直线EF分别与直线AB，CD相交于点G，H，已知∠1=∠2=50°，GM平分∠HGB交直线CD于点M，则∠3等于（）

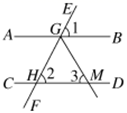A、60° B、65° C、70° D、130°

查看试题解析
6. 如图，长方形纸片ABCD中，点E是AD的中点，且AE＝1，BE的垂直平分线MN恰好过C.则长方形的一边CD的长度为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

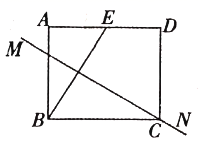查看试题解析
7. 将直线y＝－x＋a的图象向下平移2个单位后经过点A（3，3），则a的值为（）

A、－2 B、2 C、－4 D、8

查看试题解析
8. 如图，已知一次函数y＝ax＋b和y＝kx的图象相交于点P，则根据图象可得二元一次方程组 ${\begin{array}{l} y = a x + b \\ k x - y = 0 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 4 \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = 4 \\ y = 4 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 2 \end{array}$

查看试题解析
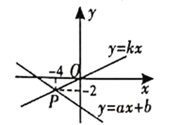9. 在平面直角坐标系中，若点P（m＋3，－2m）到两坐标轴的距离相等，则m的值为（）

A、－1 B、3 C、－1或3 D、－1或5

查看试题解析
10. 某班同学从学校出发去太阳岛春游，大部分同学乘坐大客车先出发，余下的同学乘坐小轿车20分钟后出发，沿同一路线行驶.大客车中途停车等候5分钟，小轿车赶上来之后，大客车以原速度的 $\frac{10}{7}$ 继续行驶，小轿车保持速度不变.两车距学校的路程S（单位：km）和大客车行驶的时间t（单位：min）之间的函数关系如图所示.下列说法中正确的个数是（）
①学校到景点的路程为40km；②小轿车的速度是1km/min；③a＝15；④当小轿车驶到景点入口时，大客车还需要10分钟才能到达景点入口.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在 $- \frac{1}{3}$ ， $0$ ， $π$ ， $\sqrt{2}$ ， $0.3245$ 这五个数中，无理数有个.

查看试题解析
12. 将“对顶角相等”改写为“如果...那么...”的形式，可写为.

查看试题解析
13. 生命在于运动，小张同学用手机软件记录了4月份每天行走的步数（单位：万步），将记录结果绘制成如下图所示的统计图.在这组数据中，众数是万步.

查看试题解析
14. 如图，一只蚂蚁从长为7cm、宽为5cm，高是9cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是cm.

查看试题解析

三、解答题

15. 计算： $(\sqrt{10} - 2 \sqrt{2}) (\sqrt{10} + 2 \sqrt{2}) - | \sqrt{5} - 4 | + \sqrt{20} \times \frac{1}{2}$

查看试题解析
16. 解方程组： ${\begin{array}{l} x - 2 y = 1 ① \\ 2 x + 3 y = 16 ② \end{array}$

查看试题解析
17. 公司招聘人才，对应聘者分别进行了阅读能力、思维能力和表达能力三项测试，其中甲、乙两人的测试成绩（百分制）如下表：（单位：分）

应聘者

阅读能力

思维能力

表达能力

甲

85

90

80

乙

95

80

95

若将阅读能力、思维能力和表达能力三项测试得分按1∶3∶1的比确定每人的最后成绩，谁将被录用?

查看试题解析
18. 如图，CE是△ABC的外角∠ACD的平分线，交BA的延长线于点E，已知∠B＝25°，∠E＝30°，求∠BAC的度数.

查看试题解析
19. 已知2a+1的平方根是±3，3a+2b-4的立方根是-2，求4a-5b+8的立方根.

查看试题解析
20. 如图，直线l₁：y＝kx＋4（k关0）与x轴，y轴分别相交于点A，B，与直线l₂：y＝mx（m≠0）相交于点C（1，2）.

(1)、求k，m的值；

(2)、求点A和点B的坐标.

查看试题解析
21. 如图，已知△ABC的其中两个顶点分别为：A（－4，1）、B（－2，4）.

（ 1 ）请根据题意，在图中建立平面直角坐标系，并写出点C的坐标；

（ 2 ）若△ABC每个点的横坐标保持不变，纵坐标分别乘－1，顺次连接这些点，得到△A₁B₁C₁ ，画出△A₁B₁C₁ ，判断△A₁B₁C₁与△ABC有怎样的位置关系?并写出点B的对应点B₁的坐标.

查看试题解析
22. 如图，在△ABC中，AC＝6，BC＝8，DE是△ABD的边AB上的高，且DE＝4，AD＝ $2 \sqrt{5}$ ，BD＝ $4 \sqrt{5}$ .求证：△ABC是直角三角形.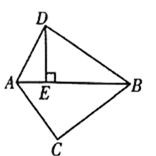

查看试题解析

23. 某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，小宇根据他们的成绩（单位：环）绘制了如下尚不完整的统计表：

	第1次	第2次	第3次	第4次	第5次
甲成绩	9	4	7	a	6
乙成绩	7	5	7	4	7

(1)、若甲成绩的平均数为6环，求a的值；

(2)、若甲成绩的方差为3.6，请计算乙成绩的方差并说明谁的成绩更稳定?

查看试题解析

24. 如图，已知∠ABC＝∠ADC，AB∥CD，E为射线BC上一点，AE平分∠BAD.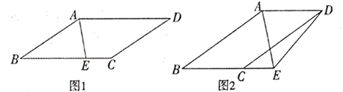

(1)、如图1，当点E在线段BC上时，求证：∠BAE＝∠BEA.

(2)、如图2，当点E在线段BC延长线上时，连接DE，若∠ADE＝3∠CDE，∠AED＝60°，求∠CED的度数.

查看试题解析
25. 在“一带一路”战略的影响下，某茶叶经销商准备把“茶路”融入“丝路”，经计算，他销售10斤A级别和20斤B级别茶叶的利润为4000元，销售20斤A级别和10斤B级别茶叶的利润为3500元

(1)、分别求出每斤A级别茶叶和每斤B级别茶叶的销售利润；

(2)、若该经销商一次购进两种级别的茶叶共200斤用于出口.设购买A级别茶叶a斤（70≤a≤120），销售完A、B两种级别茶叶后获利w元.
①求出w与a之间的函数关系式；

②该经销商购进A、B两种级别茶叶各多少斤时，才能获取最大的利润，最大利润是多少?

查看试题解析

应聘者	阅读能力	思维能力	表达能力
甲	85	90	80
乙	95	80	95