陕西省渭南市临渭区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-20 类型:期末考试
一、单选题
-
1. 9的平方根是( )A、3 B、 C、±3 D、2. 下列各组线段中,能够组成直角三角形的一组是( )A、1,2,3 B、2,3,4 C、4,5,6 D、1, ,23. 下列四个命题中,真命题有( )
两条直线被第三条直线所截,内错角相等; 如果 和 是对顶角,那么 ; 三角形的一个外角大于任何一个内角; 若 ,则 .
A、1个 B、2个 C、3个 D、4个4. 直线 过点 , ,则 的值是( )A、 B、 C、 D、5. 将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( ) A、45° B、50° C、60° D、75°6. 《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系,在其方程章中有一道题:今有甲乙二人,不知其钱包里有多少钱,若乙把其钱的一半给甲,则甲的钱数为50;若甲把其钱的 给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为x,乙持钱为y,则可列方程组
A、45° B、50° C、60° D、75°6. 《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系,在其方程章中有一道题:今有甲乙二人,不知其钱包里有多少钱,若乙把其钱的一半给甲,则甲的钱数为50;若甲把其钱的 给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为x,乙持钱为y,则可列方程组 A、 B、 C、 D、7. 在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差8. 已知函数 的部分函数值如下表所示,则该函数的图象不经过( )
A、 B、 C、 D、7. 在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差8. 已知函数 的部分函数值如下表所示,则该函数的图象不经过( )…
-2
-1
0
1
…
…
0
3
6
9
…
A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )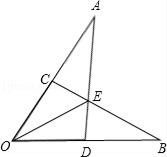 A、2对 B、3对 C、4对 D、5对10. 1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中 , , ,则下面结论错误的是( )
A、2对 B、3对 C、4对 D、5对10. 1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中 , , ,则下面结论错误的是( ) A、 B、 C、 D、 是等腰直角三角形
A、 B、 C、 D、 是等腰直角三角形二、填空题
-
11. 比较大小: .12. 如图,已知 ,直线 分别交 , 于点 , , 平分 ,若 ,则 的度数为.
 13. 以方程组 的解为坐标的点 在第象限.14. 如图,在长方形纸片 中, , ,拆叠纸片 ,使顶点 落在边 上的点 处,折痕分别交边 、 于点 、 ,则 的面积最大值是.
13. 以方程组 的解为坐标的点 在第象限.14. 如图,在长方形纸片 中, , ,拆叠纸片 ,使顶点 落在边 上的点 处,折痕分别交边 、 于点 、 ,则 的面积最大值是.
三、解答题
-
15. 计算:(1)、(2)、16. 解二元一次方程组:17. 已知在平面直角坐标系中有三点 、 , .请回答如下问题:

( 1 )在平面直角坐标系内描出点 、 、 的位置,并求 的面积;
( 2 )在平面直角坐标系中画出 ,使它与 关于 轴对称,并写出 三顶点的坐标;
( 3 )若 是 内部任意一点,请直接写出这点在 内部的对应点 的坐标.
18. 如图, 是等边三角形, 、 、 分别是 、 、 上一点,且 . (1)、若 ,求 ;(2)、如图2,连接 ,若 ,求证: .19. 某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?
(1)、若 ,求 ;(2)、如图2,连接 ,若 ,求证: .19. 某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元? 20. 节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水 与滴水时间 的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
20. 节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水 与滴水时间 的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
 (1)、容器内原有水多少升.(2)、求 与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.21. 如图,在 中, , ,点 在 上,且 , .
(1)、容器内原有水多少升.(2)、求 与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.21. 如图,在 中, , ,点 在 上,且 , . (1)、求证: ;(2)、求 的长.22. 第16届省运会在我市隆重举行,推动了我市各校体育活动如火如荼的开展,在某校射箭队的一次训练中,甲,乙两名运动员前5箭的平均成绩相同,教练将两人的成绩绘制成如下尚不完整的统计图表.
(1)、求证: ;(2)、求 的长.22. 第16届省运会在我市隆重举行,推动了我市各校体育活动如火如荼的开展,在某校射箭队的一次训练中,甲,乙两名运动员前5箭的平均成绩相同,教练将两人的成绩绘制成如下尚不完整的统计图表.
乙运动员成绩统计表(单位:环)
第1次
第2次
第3次
第4次
第5次
8
10
8
6
(1)、甲运动员前5箭射击成绩的众数是环,中位数是环;(2)、求乙运动员第5次的成绩;(3)、如果从中选择一个成绩稳定的运动员参加全市中学生比赛,你认为应选谁去?请说明理由.23. 爸爸想送小明一个书包和一辆自行车作为新年礼物,在甲、乙两商场都发现同款的自行车单价相同,书包单价也相同,自行车和书包单价之和为452元,且自行车的单价比书包的单价4倍少8元.(1)、求自行车和书包单价各为多少元;(2)、新年来临赶上商家促销,乙商场所有商品打八五折(即8.5折)销售,甲全场购物毎满100元返购物券30元(即不足100元不返券,满100元送30元购物券,满200元送60元购物券),并可当场用于购物,购物券全场通用.但爸爸只带了400元钱,如果他只在同一家商场购买看中的两样物品,在哪一家买更省钱?24. 如图,直线 与 轴、 轴分别相交于点 、 ,与直线 相交于点 .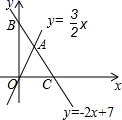 (1)、求 点坐标;(2)、如果在 轴上存在一点 ,使 是以 为底边的等腰三角形,求 点坐标;(3)、在直线 上是否存在点 ,使 的面积等于6?若存在,请求出 点的坐标,若不存在,请说明理由.
(1)、求 点坐标;(2)、如果在 轴上存在一点 ,使 是以 为底边的等腰三角形,求 点坐标;(3)、在直线 上是否存在点 ,使 的面积等于6?若存在,请求出 点的坐标,若不存在,请说明理由.