陕西省宝鸡市凤翔县2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-11-20 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、2 B、±2 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
2. 一组数据1、2、4、4、3的众数为4，则这组数据的中位数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 下列函数中， $y$ 随 $x$ 值增大而增大的是：① $y = 8 x - 7$ ；② $y = 6 - 5 x$ ；③ $y = - 8 + \sqrt{3} x$ ；④ $y = (\sqrt{5} - \sqrt{7}) x$ ；⑤ $y = 9 x$ ；⑥ $y = - 10 x$ （）

A、①②③ B、③④⑤ C、②④⑤ D、①③⑤

查看试题解析
4. 将三角形三个顶点的横坐标都加 $3$ ，纵坐标不变，则所得三角形与原三角形的关系是（）

A、将原图向左平移三个单位 B、关于原点对称 C、将原图向右平移三个单位 D、关于 $y$ 轴对称

查看试题解析
5. 能说明命题“对于任何实数a，a²≥a”是假命题的一个反例可以是（）

A、 $a = - 2$ B、 $a = 1$ C、 $a = 0$ D、 $a = 0.2$

查看试题解析
6. 若实数 $k$ 、 $b$ 满足 $k + b = 0$ ，且 $k > b$ ，则一次函数 $y = k x + b$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 如图， $O P / / Q R / / S T$ 下列各式中正确的是（）

A、 $∠ 1 + ∠ 2 + ∠ 3 = 180^{\circ}$ B、 $∠ 1 + ∠ 2 - ∠ 3 = 90^{\circ}$ C、 $∠ 1 - ∠ 2 + ∠ 3 = 90^{\circ}$ D、 $∠ 2 + ∠ 3 - ∠ 1 = 180^{\circ}$

查看试题解析
8. 已知二元一次方程组 ${\begin{array}{l} x + y = 5 \\ 2 x - y = 1 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，则一次函数 $y = - x + 5$ 与 $y = 2 x - 1$ 的图象的交点坐标为（）

A、 $(2, 3)$ B、 $(3, 2)$ C、 $(- 2, 3)$ D、 $(2, - 3)$

查看试题解析
9. 我国古代数学名著《孙子算经》记载一道题，大意为100个和尚吃了100个馒头，已知1个大和尚吃3个馒头，3个小和尚吃1个馒头，问有几个大和尚，几个小和尚？若设有 $m$ 个大和尚， $n$ 个小和尚，那么可列方程组为（）

A、 ${\begin{array}{l} m + n = 100 \\ 3 m + 3 n = 100 \end{array}$ B、 ${\begin{array}{l} m + n = 100 \\ m + 3 n = 100 \end{array}$ C、 ${\begin{array}{l} m + n = 100 \\ 3 m + \frac{n}{3} = 100 \end{array}$ D、 ${\begin{array}{l} m + n = 100 \\ 3 m + n = 100 \end{array}$

查看试题解析
10. 正方形 $A B C D$ 的边长为1，其面积记为 $S_{1}$ ，以 $C D$ 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积为 $S_{2}$ ，…按此规律继续下去，则 $S_{5}$ 的值为（）

A、 ${(\frac{1}{2})}^{4}$ B、 ${(\frac{1}{2})}^{3}$ C、 ${(\frac{\sqrt{2}}{2})}^{4}$ D、 ${(\frac{\sqrt{2}}{2})}^{3}$

查看试题解析

二、填空题

11. 直线 $y = 2 x + b$ 与 $y$ 轴的交点坐标是( $0$ ， $2$ )，则直线 $y = 2 x + b$ 与坐标轴围成的三角形面积是.

查看试题解析
12. 某学生数学学科课堂表现为 $95$ 分，平时作业为 $92$ 分，期末考试为 $90$ 分，若这三项成绩分别按 $30 %$ ， $30 %$ ， $40 %$ 的比例计入总评成绩，则该学生数学学科总评成绩是分.

查看试题解析
13. 若一次函数 $y = k x + b$ （ $k \neq 0$ ）与一次函数 $y = \frac{1}{2} x - 1$ 的图象关于 $x$ 轴对称，且交点在 $x$ 轴上.则这个函数的表达式为

查看试题解析
14. 如图，在 $Δ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ B A C$ 的平分线， $D E$ ⊥ $A B$ 于点 $E$ ，点 $F$ 在 $A C$ 上， $B D = D F$ ，若 $A F = 3$ ， $B E = 1$ ，则 $D E$ 的长为.

查看试题解析

三、解答题

15. 计算：

(1)、 $(\sqrt{2} - 2 \sqrt{3}) (2 \sqrt{3} + \sqrt{2})$

(2)、 $\sqrt{24} \times \sqrt{\frac{1}{3}} + 4 \times \sqrt{\frac{1}{8}} \times {(1 - \sqrt{2})}^{0}$

查看试题解析
16. 解方程组：

(1)、 ${\begin{array}{l} 3 x - 2 y = 8 \\ 3 x + 2 y = 10 \end{array}$

(2)、 ${\begin{array}{l} \frac{x + y}{3} + \frac{x - y}{2} = 6 \\ 3 (x + y) - 2 (x - y) = 28 \end{array}$

查看试题解析
17. 先化简，再求值： $[{(x - 3 y)}^{2} - 9 y^{2} + 2 x y] \div 2 x$ ，其中 $x ， y$ 满足 $\sqrt{x - 2} + | y + 1 | = 0$

查看试题解析
18. 已知，如图所示，在长方形ABCD中，AB=4，BC=3．

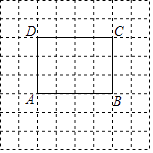
(1)、建立适当的平面直角坐标系，直接写出顶点A、B、C、D的坐标；

(2)、写出顶点C关于直线AB对称的点E的坐标．

查看试题解析
19.
如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．∠1=∠2，试判断DG与BC的位置关系，并说明理由．

查看试题解析
20. 为提高学生综合素质，亲近自然，励志青春，某学校组织学生举行“远足研学”活动，先以每小时6千米的速度走平路，后又以每小时3千米的速度上坡，共用了3小时；原路返回时，以每小时5千米的速度下坡，又以每小时4千米的速度走平路，共用了4小时，问平路和坡路各有多远.

查看试题解析

21. 甲、乙两名学生参加数学素质测试（有四项），每项测试成绩采用百分制，成绩如表

：

学生	数与代数	空间与图形	统计与概率	综合与实践	平均成绩	方差
甲	87	93	85	91	89
乙	89	96	80	91		33.5

(1)、请计算甲的四项成绩的方差和乙的平均成绩；

(2)、若数与代数、空间与图形、统计与概率、综合与实践的成绩按

4 : 3 : 2 : 1

计算，哪个学生数学综合素质测试成绩更好？请说明理由.

查看试题解析

22. 某工厂要把一批产品从 $A$ 地运往 $B$ 地，若通过铁路运输，则每千米需交运费20元，还要交装卸费400元及手续费200元，若通过公路运输，则每千米需要交运费30元，还需交手续费100元（由于本厂职工装卸，不需交装卸费）.设 $A$ 地到 $B$ 地的路程为 $x k m$ ，通过铁路运输和通过公路运输需交总运费 $y_{1}$ 元和 $y_{2}$ 元.

(1)、求 $y_{1}$ 和 $y_{2}$ 关于 $x$ 的函数表达式.

(2)、若 $A$ 地到 $B$ 地的路程为 $120 k m$ ，哪种运输可以节省总运费？

查看试题解析
23. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ，将 $R t Δ A B C$ 绕点A顺时针旋转到 $R t Δ A D E$ 的位置，点E在斜边AB上，连结BD，过点D作 $D F ⊥ A C$ 于点F.

(1)、如图1，若点F与点A重合.①求证： $A C = B C$ ；②若 $A C = \sqrt{2}$ ，求出 $B D^{2}$ ；

(2)、若 $∠ D A F = ∠ A B D$ ，如图2，当点F在线段CA的延长线上时，判断线段AF与线段AB的数量关系.并说明理由.

查看试题解析