广西壮族自治区百色市平果县2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-11-20 类型：期末考试

进入出卷网下载

一、单选题

1. 点A(－1，2)在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 如图，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
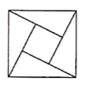3. 一次函数y=x+2的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 有下列长度的三条线段，能组成三角形的是（）

A、2cm，3cm，4cm B、1cm，4cm，2cm C、1cm，2cm，3cm D、6cm，2cm，3cm

查看试题解析
5. 将点 $A (2, - 1)$ 向左平移 $3$ 个单位长度，在向上平移 $4$ 个单位长度得到点 $B$ ，则点 $B$ 的坐标是（）

A、 $(5, 3)$ B、 $(5, - 5)$ C、 $(- 1, - 5)$ D、 $(- 1, 3)$

查看试题解析
6. 对于一次函数y＝（k﹣3）x+2，y随x的增大而增大，k的取值范围是（）

A、k＜0 B、k＞0 C、k＜3 D、k＞3

查看试题解析
7. 下列图象中，不能表示y是x的函数的是（）

A、 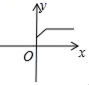B、 C、 D、

查看试题解析
8. 如图，函数y=ax+b和y=kx的图象交于点P，关于x，y的方程组 ${\begin{array}{l} y - a x = b \\ k x - y = 0 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = - 3 \end{array}$ B、 ${\begin{array}{l} x = - 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = - 3 \\ y = - 2 \end{array}$

查看试题解析
9. 如图，在△ABC中，∠ACB=100°，∠A=20°，D是AB上一点，将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（　　）

A、40° B、20° C、55° D、30

查看试题解析
10. 下列命题是真命题的是（）

A、一个三角形中至少有两个锐角 B、若∠A与∠B是内错角，则 $∠ A = ∠ B$ C、如果两个角有公共边，那么这两个角一定是邻补角 D、如果 $3.14 a = πb$ ，那么 $a = b$

查看试题解析
11. 如图，已知△ABC是等腰三角形，AB=AC，点O是BC上任意一点，OE⊥AB，OF⊥AC，等腰三角形的腰长为4，面积为4 $\sqrt{3}$ ，则OE+OF的值为（）

A、1.5 B、2 $\sqrt{3}$ C、2.5 D、3

查看试题解析
12. 已知A，B两地相距120千米，甲乙两人沿同一条公路匀速行驶，甲骑自行车以20千米/时从A地前往B地，同时乙骑摩托车从B地前往A地，设两人之间的距离为s（千米），甲行驶的时间为t（小时），若s与t的函数关系如图所示，则下列说法错误的是（）

A、经过2小时两人相遇 B、若乙行驶的路程是甲的2倍，则t=3 C、当乙到达终点时，甲离终点还有60千米 D、若两人相距90千米，则t=0.5或t=4.5

查看试题解析

二、填空题

13. 平面直角坐标系中，点A和点B（1，﹣2）关于y轴对称，则点A的坐标是．

查看试题解析
14. 等腰三角形的一个角100°，它的另外两个角的度数分别为

查看试题解析
15. 把直线 $y = 2 x + 5$ 向下平移个单位得到直线 $y = 2 x - 1$ .

查看试题解析
16. 若P(2－a，2a+3)到两坐标轴的距离相等，则点P的坐标是.

查看试题解析
17. 已知点A(x₁ ， y₁)、B(x₂ ， y₂)在直线y=-2x+b上，当x₁<x₂时，y₁与y₂的大小关系为.

查看试题解析
18. 如图，△ABC中，DH是AC的垂直平分线，交BC于P，MN是AB的垂直平分线，交BC于点Q，连接AP、AQ，已知 $∠ B A C = 72^{°}$ ，则 $∠ P A Q =$ 度.

查看试题解析

三、解答题

19. 如图，方格纸中每个小方格都是边长为1个单位长度的正方形，建立平面直角坐标系后，△ABC的顶点坐标为A(1，﹣4)，B(5，﹣4)，C(4，﹣1).

（ 1 ）在方格纸中画出△ABC；

（ 2 ）若把△ABC向上平移6个单位长度再向左平移7个单位长度得到OA'B'C，在图中画出△A'B'C'.并写出B'的坐标.

查看试题解析
20. 如图，一次函数y $= - \frac{3}{4}$ x+6与坐标轴交于A、B两点，求点A、B的坐标.

查看试题解析
21. 如图，在△ABC中，∠B、∠C的平分线BE，CD相交于点F．

(1)、∠ABC＝40°，∠A＝60°，求∠BFD的度数；

(2)、直接写出∠A与∠BFD的数量关系．

查看试题解析
22. 一次函数 $y = k x + 4$ 的图象过点 $(- 1, 7)$ .

(1)、求 $k$ 的值；

(2)、判断点 $(a, - 3 a + 4)$ 是否在该函数图象上，并说明理由.

查看试题解析
23. 如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，AD=5cm，DE=3cm，求BE的长.

查看试题解析
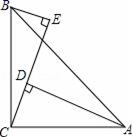24. 如图，直线y= $\frac{2}{3}$ x+4与x轴相交于点A，与y轴相交于点B.

(1)、求△AOB的面积；

(2)、过B点作直线BC与x轴相交于点C，若△ABC的面积是16，求点C的坐标.

查看试题解析
25. 如图，已知直线y=kx+b交x轴于点A，交y轴于点B，直线y=2x﹣4交x轴于点D，与直线AB相交于点C（3，2）．

(1)、根据图象，写出关于x的不等式2x﹣4＞kx+b的解集；

(2)、若点A的坐标为（5，0），求直线AB的解析式；

(3)、在（2）的条件下，求四边形BODC的面积．

查看试题解析
26. 2019年北疆承办了世界园艺博览会，某商店为了抓住博览会的商机，决定购买A.B两种世园会纪念品，若购进A中纪念品20件，B种纪念品10件，需要2000元;若购进A中纪念品8件，B种纪念品6件，需要1100元.

(1)、求购进A.B两种纪念品每件各需要多少元?

(2)、若该商店决定拿出10000元全部用来购进这两种纪念品，考虑到市场需求，要求购进A种纪念品的数量不少于B种的6倍，且少于B种纪念品数量的8倍，设购进B种纪念品a件，则该商店共有几种进货方案?

(3)、在第(2)问的条件下，若销售每件A种纪念品可获利润30元，每件B种纪念品可获利润40元，设总利润为y元，请写出总利润y(元)与a(个)的函数关系式，并根据函数关系式说明总利润最高时的进货方案.

查看试题解析