广西玉林市陆川县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-20 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )
2. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )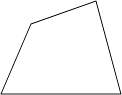 A、0根 B、1根 C、2根 D、3根3. 如图, 已知△ABE≌△ACD,∠1=∠2,∠B=∠C,则下列等式不正确的是( )
A、0根 B、1根 C、2根 D、3根3. 如图, 已知△ABE≌△ACD,∠1=∠2,∠B=∠C,则下列等式不正确的是( )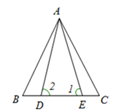 A、AB=AC B、BE=DC C、AD=DE D、∠BAE= ∠CAD4. 如图,△ABC中,DE是AC的垂直平分线,AE= 5cm,△ABD的周长为16cm,则△ABC的周长为( )
A、AB=AC B、BE=DC C、AD=DE D、∠BAE= ∠CAD4. 如图,△ABC中,DE是AC的垂直平分线,AE= 5cm,△ABD的周长为16cm,则△ABC的周长为( )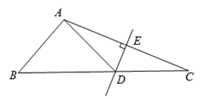 A、21cm B、26cm C、28cm D、31cm5. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A、21cm B、26cm C、28cm D、31cm5. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )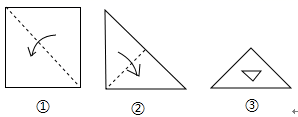 A、
A、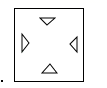 B、
B、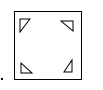 C、
C、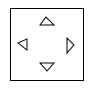 D、
D、 6. 下面是某同学在一次作业中的所做的部分试题:①3m+2n=5mn;② ;③ ; ④ ; ⑤ ⑥ ,其中正确的有( )A、5个 B、4个 C、3个 D、2个7. 解分式方程 ,分以下四步,其中错误的一步是( )A、方程两边各分式的最简公分母是 B、方程两边都乘以 ,得整式方程: C、解这个整式方程,得 D、原方程的解为8. (x-m)2=x2+nx+36,则n的值为( )A、12 B、-12 C、-6 D、±129.
6. 下面是某同学在一次作业中的所做的部分试题:①3m+2n=5mn;② ;③ ; ④ ; ⑤ ⑥ ,其中正确的有( )A、5个 B、4个 C、3个 D、2个7. 解分式方程 ,分以下四步,其中错误的一步是( )A、方程两边各分式的最简公分母是 B、方程两边都乘以 ,得整式方程: C、解这个整式方程,得 D、原方程的解为8. (x-m)2=x2+nx+36,则n的值为( )A、12 B、-12 C、-6 D、±129.如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
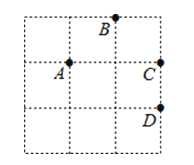 A、A点 B、B点 C、C点 D、D点10. 设 是三角形的三边长,且满足 ,关于此三角形的形状有以下判断:①是直角三角形; ②是等边三角形; ③是锐角三角形;④是钝角三角形,其中正确的说法的个数有( )A、1个 B、2个 C、3个 D、4个11. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且12. 如图,在△ABD中,AD=AB,∠DAB=90⁰,在△ACE中,AC=AE,∠EAC=90⁰,CD,BE相交于点F,有下列四个结论:①DC=BE;②∠BDC=∠BEC;③DC⊥BE;④FA平分∠DFE.其中,正确的结论有( )
A、A点 B、B点 C、C点 D、D点10. 设 是三角形的三边长,且满足 ,关于此三角形的形状有以下判断:①是直角三角形; ②是等边三角形; ③是锐角三角形;④是钝角三角形,其中正确的说法的个数有( )A、1个 B、2个 C、3个 D、4个11. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且12. 如图,在△ABD中,AD=AB,∠DAB=90⁰,在△ACE中,AC=AE,∠EAC=90⁰,CD,BE相交于点F,有下列四个结论:①DC=BE;②∠BDC=∠BEC;③DC⊥BE;④FA平分∠DFE.其中,正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 某种电子元件的面积大约为0.00000069平方毫米,将0.00000069这个数用科学记数法表示为 .14. 如图所示,已知∠1=22°,∠2=28°,∠A=56°,则∠BOC的度数是.
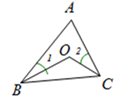 15. 如图,△ABC的三边AB,BC,CA的长分别为14,12,8,其三条角平分线的交点为O,则 .
15. 如图,△ABC的三边AB,BC,CA的长分别为14,12,8,其三条角平分线的交点为O,则 .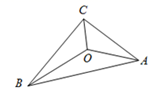 16. 若分式 的值为零,则x的值为 .
16. 若分式 的值为零,则x的值为 .
17. 已知实数m,n满足 则 =.18. 如图,等腰三角形ABC的底边BC长为8cm,面积是48 ,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为.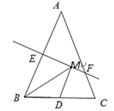
三、解答题
-
19. 计算(1)、(2)、分解因式:20. 化简 ,并求值,其中a与2、3构成△ABC的三边,且a为整数.21. 关于x的方程 有增根,求 的值.22. 如图,已知在△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
 (1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).(2)、连接AD,若∠B=38°,求∠CAD的度数.23. 求证:有两个角和其中一个角的角平分线对应相等的两个三角形全等.24. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定天数是多少天?(2)、已知甲队每天的施工费用为5500元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙合做来完成,则该工程施工费用是多少?25. 观察下列等式:
(1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).(2)、连接AD,若∠B=38°,求∠CAD的度数.23. 求证:有两个角和其中一个角的角平分线对应相等的两个三角形全等.24. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定天数是多少天?(2)、已知甲队每天的施工费用为5500元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙合做来完成,则该工程施工费用是多少?25. 观察下列等式:第1个等式: ; 第2个等式: ;
第3个等式: ; 第4个等式: ;……
请回答下列问题:
(1)、按以上规律,用含n的式子表示第n个等式: ==(n为正整数)(2)、求 的值.26. 如图,直角坐标系中,点A的坐标为(3,0),以线段OA为边在第四象限内作等边△AOB,点C为 轴正半轴上一动点(OC>3),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交 轴于点E.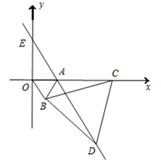 (1)、证明∠ACB=∠ADB;(2)、若以A,E,C为顶点的三角形是等腰三角形,求此时C点的坐标;(3)、随着点C位置的变化, 的值是否会发生变化?若没有变化,求出这个值;若有变化,说明理由.
(1)、证明∠ACB=∠ADB;(2)、若以A,E,C为顶点的三角形是等腰三角形,求此时C点的坐标;(3)、随着点C位置的变化, 的值是否会发生变化?若没有变化,求出这个值;若有变化,说明理由.