广西贺州市平桂区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-20 类型:期末考试
一、单选题
-
1. 点 向右平移3个单位后的坐标为( )A、 B、 C、 D、2. 当x=-1时,函数 的函数值为( )A、-2 B、-1 C、2 D、43. 用下列长度的三条线段,能组成一个三角形的是( )A、1cm,2cm,3cm B、2cm,2cm,3cm C、2cm,2cm,4cm D、5cm,6cm,12cm4. 下列图案不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列命题是假命题的是( ).A、两直线平行,内错角相等 B、三角形内角和等于180° C、对顶角相等 D、相等的角是对顶角6. 等腰三角形是轴对称图形,它的对称轴是( )A、中线 B、底边上的中线 C、中线所在的直线 D、底边上的中线所在的直线7. 已知:C、D是线段AB外的两点,AC=BC,AD=BD,点P在直线CD上,若AP=5,则BP的长为( )A、2.5 B、5 C、10 D、258. 一次函数 的图象经过点 ,则该函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,∠MCN=42°,点P在∠MCN内部,PA⊥CM,PB⊥CN,垂足分别为A、B,PA=PB,则∠MCP的度数为( ).
5. 下列命题是假命题的是( ).A、两直线平行,内错角相等 B、三角形内角和等于180° C、对顶角相等 D、相等的角是对顶角6. 等腰三角形是轴对称图形,它的对称轴是( )A、中线 B、底边上的中线 C、中线所在的直线 D、底边上的中线所在的直线7. 已知:C、D是线段AB外的两点,AC=BC,AD=BD,点P在直线CD上,若AP=5,则BP的长为( )A、2.5 B、5 C、10 D、258. 一次函数 的图象经过点 ,则该函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,∠MCN=42°,点P在∠MCN内部,PA⊥CM,PB⊥CN,垂足分别为A、B,PA=PB,则∠MCP的度数为( ). A、21° B、24° C、42° D、48°10. 已知函数 和 ,当时 , 的取值范围是( )A、 B、 C、 D、11. 如图,在△ABC中,∠C=63°,AD是BC边上的高,AD=BD,点E在AC上,BE交AD于点F,BF=AC,则∠AFB的度数为( ).
A、21° B、24° C、42° D、48°10. 已知函数 和 ,当时 , 的取值范围是( )A、 B、 C、 D、11. 如图,在△ABC中,∠C=63°,AD是BC边上的高,AD=BD,点E在AC上,BE交AD于点F,BF=AC,则∠AFB的度数为( ). A、27° B、37° C、63° D、117°12. 已知:如图, 是 的中线, ,点 为垂足, ,则 的长为( )
A、27° B、37° C、63° D、117°12. 已知:如图, 是 的中线, ,点 为垂足, ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 点P(-2,3)在第象限.14. 函数y= 自变量x的取值范围是 .15. 在△ABC中,AB=AC,∠B=60°,则△ABC是三角形.16. “同位角相等”的逆命题是 .
17. 已知:如图,点 在同一直线上, , ,则 .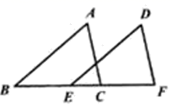 18. 已知:如图,点 分别在等边三角形 的边 的延长线上, 的延长线交 于点 ,则 .
18. 已知:如图,点 分别在等边三角形 的边 的延长线上, 的延长线交 于点 ,则 .
三、解答题
-
19. △ABC在直角坐标系中如图所示,请写出点A、B、C的坐标.
 20. 已知函数 ,(1)、 为何值时,该函数是一次函数(2)、 为何值时,该函数是正比例函数.21. 多边形ABCD在直角坐标系中如图所示,在图中分别作出它关于x轴y轴的对称图形.
20. 已知函数 ,(1)、 为何值时,该函数是一次函数(2)、 为何值时,该函数是正比例函数.21. 多边形ABCD在直角坐标系中如图所示,在图中分别作出它关于x轴y轴的对称图形. 22. 补充下列证明,并在括号内填上推理依据.
22. 补充下列证明,并在括号内填上推理依据.已知:如图,在 中, 平分 交 于点 , 交 于点 ,且 ,求证: .

证明: ,( ).
,
.( ),
_▲__ _▲_.
平分 ,
( ),
,
,
_▲__ _▲__ ,
.( ).
23. 已知:如图, , (1)、求证: .(2)、求 的长.
(1)、求证: .(2)、求 的长.


