浙江省永嘉县十校2020-2021学年八年级上学期数学期中联考试卷
试卷更新日期:2020-11-20 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、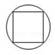 D、
D、 2. 三角形的两边长为2和3,则第三边长可以为( )A、1 B、4 C、5 D、63. 下列命题是真命题的是( )A、内错角相等 B、直角三角形的两个锐角互补 C、三角形三个内角的和等于180° D、有一个角是60°的三角形是等边三角形4. 在数轴上表示不等式2x-4≥0的解集,正确的是( )A、
2. 三角形的两边长为2和3,则第三边长可以为( )A、1 B、4 C、5 D、63. 下列命题是真命题的是( )A、内错角相等 B、直角三角形的两个锐角互补 C、三角形三个内角的和等于180° D、有一个角是60°的三角形是等边三角形4. 在数轴上表示不等式2x-4≥0的解集,正确的是( )A、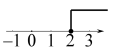 B、
B、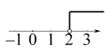 C、
C、 D、
D、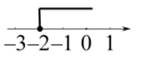 5. 如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=40°,∠E=30°,则∠ACB的度数为( )
5. 如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=40°,∠E=30°,则∠ACB的度数为( )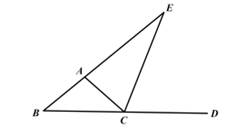 A、30° B、35° C、40° D、70°6. 在△ABC中,∠A,∠B,∠C的对应边为a、b、c,下列条件不能判断△ABC为直角三角形的是( )A、∠A:∠B:∠C=1: 2: 3 B、∠A+∠B=∠C C、a=6,b=8, c=10 D、a= , b=2,c=7. 如图,AB平分∠CAD,根据下列条件,不一定能判定△ACB≌△ADB的是( )
A、30° B、35° C、40° D、70°6. 在△ABC中,∠A,∠B,∠C的对应边为a、b、c,下列条件不能判断△ABC为直角三角形的是( )A、∠A:∠B:∠C=1: 2: 3 B、∠A+∠B=∠C C、a=6,b=8, c=10 D、a= , b=2,c=7. 如图,AB平分∠CAD,根据下列条件,不一定能判定△ACB≌△ADB的是( )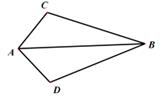 A、AC=AD B、∠ABC=∠ABD C、∠C=∠D D、BC=BD8. 如图,BE是△ABC的角平分线,AD⊥BC于点D,交BE于点F,EA=EF,若∠C=40°,则∠BAD的度数是( )
A、AC=AD B、∠ABC=∠ABD C、∠C=∠D D、BC=BD8. 如图,BE是△ABC的角平分线,AD⊥BC于点D,交BE于点F,EA=EF,若∠C=40°,则∠BAD的度数是( )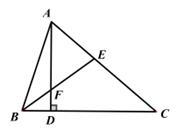 A、10° B、12° C、15° D、18°9. 如图,在△ABC中,AB=AC,∠BAC=60°,BC=2,AD⊥BC于D,点F是AB的中点,点E在AD边上,则BE+EF的最小值是( )
A、10° B、12° C、15° D、18°9. 如图,在△ABC中,AB=AC,∠BAC=60°,BC=2,AD⊥BC于D,点F是AB的中点,点E在AD边上,则BE+EF的最小值是( )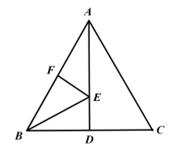 A、1 B、 C、2 D、10. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂0A=OB=10分米,晾衣臂支架HG=FE=5分米,HO=FO=4分米。当∠AOC=90°,且OB∥CD时,线段OG与OE的长分别为( )
A、1 B、 C、2 D、10. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂0A=OB=10分米,晾衣臂支架HG=FE=5分米,HO=FO=4分米。当∠AOC=90°,且OB∥CD时,线段OG与OE的长分别为( )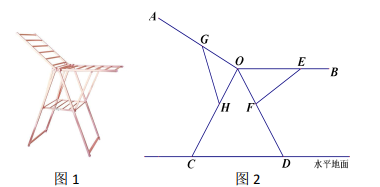 A、3和7 B、3和 C、3和2+ D、 和2+
A、3和7 B、3和 C、3和2+ D、 和2+二、填空题(每题3分,共24分)
-
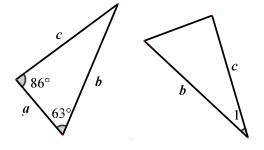
11. 命题“同位角相等”的逆命题为。12. 用不等式表示“x与y的差不大于2”: 。13. 如图,两个三角形全等,图中的字母表示三角形的边长,则∠1= 。
 14. 如图所示,△ABC为边长为4的等边三角形,AD为BC边上的高,以AD为边的正方形ADEF的面积为。
14. 如图所示,△ABC为边长为4的等边三角形,AD为BC边上的高,以AD为边的正方形ADEF的面积为。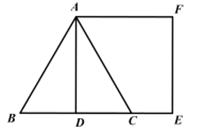 15. 如图,每个小正方形的边长为1,A,B,C恰好是小正方形的顶点,则∠BAC=。
15. 如图,每个小正方形的边长为1,A,B,C恰好是小正方形的顶点,则∠BAC=。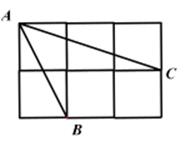 16. 已知a,b为三角形的两条边长,且a,b满足(a-6)2+|8-b|=0,若该三角形为等腰三角形,则该三角形的周长为。17. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线DE交AB于点E,交BC于点D,AC=6,BC=8,则DE的长为=。
16. 已知a,b为三角形的两条边长,且a,b满足(a-6)2+|8-b|=0,若该三角形为等腰三角形,则该三角形的周长为。17. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线DE交AB于点E,交BC于点D,AC=6,BC=8,则DE的长为=。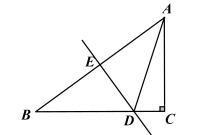 18. 如图,在△ABC中,∠C=90°,∠B=30°,D是斜边AB的中点,P是边BC上的点,且PC=AC= ,以AP为边在AP右侧作等边 △APQ ,连结DQ,则DQ=;连结PD,则PD=。
18. 如图,在△ABC中,∠C=90°,∠B=30°,D是斜边AB的中点,P是边BC上的点,且PC=AC= ,以AP为边在AP右侧作等边 △APQ ,连结DQ,则DQ=;连结PD,则PD=。
三、解答题(共46分)
-
19. 求出不等式 ≤6的解,并把它的解集在数轴上表示出来。
 20. 如图,在5X5的方格纸(每个小方格都是边长为1的正方形)中,我们把每个小正方形的顶点称为格点,三个顶点都在格点上的三角形称为格点三角形,点A,B均在格点上,请按下列要求画图。
20. 如图,在5X5的方格纸(每个小方格都是边长为1的正方形)中,我们把每个小正方形的顶点称为格点,三个顶点都在格点上的三角形称为格点三角形,点A,B均在格点上,请按下列要求画图。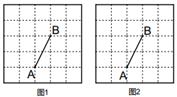 (1)、在图1中画一个面积为2的格点等腰△ABC。(2)、在图2中画一个格点等腰直角△ABD。21. 填空:已知:如图,A、D、B、E在同一直线上,AD=BE,AC∥DF且AC=DF,
(1)、在图1中画一个面积为2的格点等腰△ABC。(2)、在图2中画一个格点等腰直角△ABD。21. 填空:已知:如图,A、D、B、E在同一直线上,AD=BE,AC∥DF且AC=DF,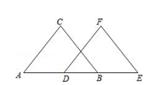
证明:BC=EF。
解:∵AD=BE
∴AD+ DB= BE+▲
即:AB=DE
∵AC∥DF
∴∠ ▲ =∠ ▲
在△ABC和△DEF中
∴△ABC≌△DEF (▲ )
∴BC=EF( ▲ )
22. 如图所示,在△ABC中,AE平分∠BAC,DE∥AC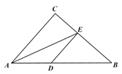 (1)、求证:△ADE是等腰三角形(2)、若∠C=90°,∠AED=25°,求∠B的度数。
(1)、求证:△ADE是等腰三角形(2)、若∠C=90°,∠AED=25°,求∠B的度数。