广东省佛山市顺德区2020-2021学年九年级上学期数学第九周测试卷
试卷更新日期:2020-11-18 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 方程x2=3x的解为( )A、x=0 B、x=3 C、x1=0,x2=-3 D、x1=0,x2=32. 下列条件中,能判定一个四边形为矩形的条件是( )A、对角线互相平分的四边形 B、对角线相等且平分的四边形 C、对角线相等的四边形 D、对角线相等且互相垂直的四边形3. 用配方法解方程 x2+4x+1=0 ,经过配方,得到( )A、(x+2)2=5 B、
 C、
C、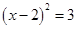 D、
D、 4. 若正方形的对角线长为2 cm,则这个正方形的面积为( )A、4 B、2 C、 D、5. 若关于x的方程x2+x-a+=0 有两个不相等的实数根,则实数a的取值范围是( )A、
4. 若正方形的对角线长为2 cm,则这个正方形的面积为( )A、4 B、2 C、 D、5. 若关于x的方程x2+x-a+=0 有两个不相等的实数根,则实数a的取值范围是( )A、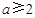 B、
B、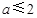 C、a>2
D、
C、a>2
D、 6. 根据下表的对应值,一元二次方程 ax2+bx+c=0 其中一个解的取值范围是( )
6. 根据下表的对应值,一元二次方程 ax2+bx+c=0 其中一个解的取值范围是( )x
1.1
1.2
1.3
1.4
ax2+bx+c
-0.59
0.84
2.29
3.76
A、1.0<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、1.3<x<1.47. 某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )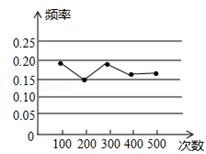 A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面的点数是48. 如图,在菱形ABCD中,对角线AC、BD相交于点O , 下列结论:①AC⊥BD;②OA =OB;③∠ADB =∠CDB;④△ABC是等边三角形,其中一定成立的是( )
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面的点数是48. 如图,在菱形ABCD中,对角线AC、BD相交于点O , 下列结论:①AC⊥BD;②OA =OB;③∠ADB =∠CDB;④△ABC是等边三角形,其中一定成立的是( ) A、①③ B、③④ C、②③ D、①②9. 初三(3)班同学在临近毕业时,每一个同学都将自己的照片向全班其他同学各送一张以表示纪念,全班共送了1640张照片,如果设全班有x名学生,则根据题意,可列方程( )A、x(x+1)=1640 B、x(x-1)=1640 C、2x(x+1)=1640 D、x(x-1)=2×164010. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )
A、①③ B、③④ C、②③ D、①②9. 初三(3)班同学在临近毕业时,每一个同学都将自己的照片向全班其他同学各送一张以表示纪念,全班共送了1640张照片,如果设全班有x名学生,则根据题意,可列方程( )A、x(x+1)=1640 B、x(x-1)=1640 C、2x(x+1)=1640 D、x(x-1)=2×164010. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ) A、1 B、2 C、
A、1 B、2 C、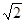 D、
D、
二、填空题(本大题共6小题,每小题4分,共24分)
-
11. 已知关于x的方程 是一元二次方程,则m的值为 .
12. 小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有只。13. 某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,若设平均每月增长的百分率为 ,根据题意可列出的方程为 .14. 直角三角形两边长分别为6cm和8cm, 则斜边上的中线长为cm.15. 游行队伍有8行12列,后又增加了69人,要使得队伍增加的行数和列数相同,需要增加行。16. 如下图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ , 那么图中矩形AMKP的面积 与矩形QCNK的面积 的大小关系是 (填“>”或“<”或“=”).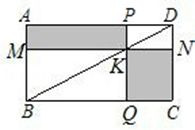 17. 如下图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y 轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OBl为边作第三个正方形OBlB2C2 , 照此规律作下去,则点B2020的纵坐标为 。
17. 如下图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y 轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OBl为边作第三个正方形OBlB2C2 , 照此规律作下去,则点B2020的纵坐标为 。
三、解答题
-
18. 解方程:19. 如图,在平行四边形ABCD中,AB < BC
 (1)、利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,留痕迹);(2)、若BC =8,CD =5,求DE的长 .20. 在长为10厘米,宽8厘米的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
(1)、利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,留痕迹);(2)、若BC =8,CD =5,求DE的长 .20. 在长为10厘米,宽8厘米的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
四、解答题
-
21. 在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下的三个小球中随机取出一个小球,记下数字为y,点Q坐标记作(x,y)。(1)、画树状图或列表,写出 Q点所有的坐标。(2)、计算由x、y确定的点Q (x,y)在函数y=-x+5图象上的概率;(3)、小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜。 这个游戏公平吗?说明理由;若不公平,怎么修改规则才对双方公平?22. 已知关于x的一元二次方程(1)、求证:这个方程有两个不相等的实数根。(2)、如果这个方程的两个实数根分别是 ,且 ,求m的值。23. 如图所示,把一张矩形纸片沿对角线折叠:
 (1)、重合部分是什么图形?请说明理由。(2)、若AB=4,BC=8,求AF.
(1)、重合部分是什么图形?请说明理由。(2)、若AB=4,BC=8,求AF.五、解答题

