广东省佛山市顺德区2020-2021学年八年级上学期数学第九周测试卷

试卷更新日期：2020-11-18 类型：月考试卷

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，共30分)在每小题列出的四个选项中，只有一个是正确的，请将下列各题的正确选项填写在答题卡相应的位置上.

1. 在下列各数 $- \sqrt{4}$ ， $\sqrt[3]{9}$ , $\frac{22}{7}$ ，0中，无理数的是（　　）

A、 $- \sqrt{4}$ ， B、 $\sqrt[3]{9}$ C、 $\frac{22}{7}$ D、0

查看试题解析
2. 下列各式中，正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{16} = \pm 4$ C、 $\sqrt[3]{- 8} = - 2$ D、 ${(- \sqrt{2})}^{2} = 4$

查看试题解析
3. 下列四组数中不能构成直角三角形的一组是（）

A、1，2， $\sqrt{6}$ B、3，5，4 C、5，12，13 D、3，2， $\sqrt{13}$

查看试题解析
4. 下列式子中，属于最简二次根式的是

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
5. 在平面直角坐标系中，已知点P的坐标是（－1，－2），则点P关于y轴对称的点的坐标是（）

A、（－1，2） B、（1，－2） C、（1，2） D、（2，1）

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{6}$ ÷ $\sqrt{3}$ ＝2 B、 $\sqrt{2}$ + $\sqrt{3}$ ＝ $\sqrt{5}$ C、 $\sqrt{12}$ ＝ $3 \sqrt{2}$ D、 $\sqrt{2}$ · $\sqrt{3}$ ＝ $\sqrt{6}$

查看试题解析
7. 如图，已知OA=OB ，那么数轴上点A所表示的数是（）

A、﹣2.4 B、2.4 C、- $\sqrt{5}$ D、 $\sqrt{5}$

查看试题解析
8. 点P(m+3，m+1)在直角坐标系的x轴上，则点P的坐标为（）

A、（0，2） B、（2，0） C、（4，0） D、（0，-2）

查看试题解析
9. 已知 $\sqrt{a - 2} + | b + 1 | = 0$ ，那么（a+b）²⁰²⁰的值为（　　）

A、﹣3²⁰²⁰ B、3²⁰²⁰ C、﹣1 D、1

查看试题解析
10. 下列说法：①π的相反数是-π；②若 $| x | = \sqrt{6}$ ，则x= $\sqrt{6}$ ；③若a为实数，则a的倒数是 $\frac{1}{a}$ ；④若 $\sqrt{x^{2}}$ =-x,则x<0.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共7小题，每小题4分，共28分）

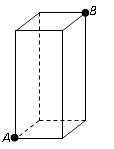
11. 16的平方根是，算术平方根是.

查看试题解析
12. 计算：（ $\sqrt{2}$ + $\sqrt{5}$ ）（ $\sqrt{2}$ - $\sqrt{5}$ ）＝

查看试题解析
13. 点A（﹣3，4）到y轴的距离为，到原点的距离为．

查看试题解析
14. 比较大小： -3 - $2 \sqrt{2}$ （用“>”　、“<”或“=”填空）。

查看试题解析
15. 已知直角三角形的三边长为6，8，x,则以x为边长的正方形的面积为

查看试题解析
16. 如图，一只蚂蚁从长、宽都是2，高是5的长方体纸盒的A点沿纸盒面爬到B点，那么它所行的最短路线的长是.

查看试题解析
17. 如图，已知点 $A (0 ， 1)$ ．规定“把点 $A$ 先作关于 $x$ 轴对称，再向左平移1个单位”为一次变换．经过第一次变换后，点 $A$ 的坐标为；经过第二次变换后，点 $A$ 的坐标为；那么连续经过2019次变换后，点 $A$ 的坐标为．

查看试题解析

三、解答题

18. 计算： $\sqrt{4} - \sqrt{6} \times \sqrt{\frac{27}{2}}$

查看试题解析
19. 如图：在△ABC中∠C=90°，AB＝3，BC＝2 ，求△ABC的面积．

查看试题解析
20. 如图，在△ABC中，AB=AC=6，BC=4．以点B为坐标原点，BC所在的直线为x轴建立平面直角坐标系．

(1)、请在图中画出符合条件的直角坐标系；

(2)、求点A的坐标．

查看试题解析

四、解答题

21. “中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米/小时，如图，一辆小汽车在一条城市街道上直道行驶，某一时刻刚好行驶到路面对车速检测仪正前方30米C处，过了2秒后，小汽车行驶到B处，测得小汽车与车速检测仪间距离为50米，

(1)、求BC的长；

(2)、这辆小汽车超速了吗？

查看试题解析
22. 已知∠ACB＝90°，BC＝ $\sqrt{6}$ ，AC＝ $\sqrt{2}$ ，CD是边AB上的高．

(1)、求CD的长．

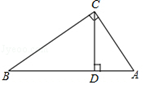(2)、求 $Δ A D C$ 的面积.

查看试题解析
23. 如图，点E在正方形ABCD内，AE=1，BE= $\sqrt{2}$ ，AB= $\sqrt{3}$ ．

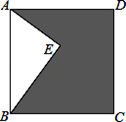(1)、△ABE是直角三角形吗？为什么？

(2)、请求出阴影部分的面积S．

查看试题解析

五、解答题

24. 先阅读，再解答：由 $(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3}) = {(\sqrt{5})}^{2} - {(\sqrt{3})}^{2} = 2$ 可以看出，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式，在进行二次根式计算时，利用有理化因式，有时可以化去分母中的根号，例如：
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ，请完成下列问题：

(1)、 $\sqrt{2} - 1$ 的有理化因式是；

(2)、化去式子分母中的根号： $\frac{3}{3 - \sqrt{6}} =$ ．（直接写结果）

(3)、 $\sqrt{2019} - \sqrt{2018}$ $\sqrt{2018} - \sqrt{2017}$ （填 $>$ 或 $<$ ）

(4)、利用你发现的规律计算下列式子的值： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2018} + \sqrt{2017}}) (\sqrt{2018} + 1)$

查看试题解析
25. 小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为 $\sqrt{5}$ 、 $\sqrt{10}$ 、 $\sqrt{13}$ ，求△ABC的面积．
小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．请回答：

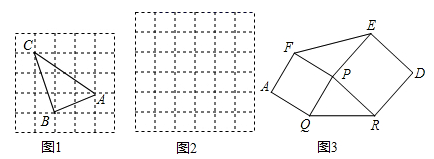(1)、求图1中△ABC的面积；

(2)、图2是一个6×6的正方形网格（每个小正方形的边长为1）．
利用构图法在答题卡的图2中画出三边长分别为 $\sqrt{13}$ 、 $2 \sqrt{5}$ 、 $\sqrt{29}$ 的格点△DEF；

(3)、图2是一个6×6的正方形网格（每个小正方形的边长为1），计算△DEF的面积是．

(4)、如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若PQ= $2 \sqrt{2}$ ，PR= $\sqrt{13}$ ，QR= $\sqrt{17}$ ，则六边形AQRDEF的面积是．

查看试题解析