广东省阳江市江城区2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期:2020-11-18 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 在下列各图形中,分别画出了△ABC中BC边上的高AD,其中正确的是( )A、
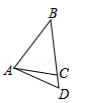 B、
B、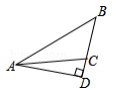 C、
C、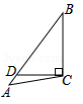 D、
D、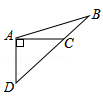 2. 如图所示,以线段BC为一边的三角形共有( )
2. 如图所示,以线段BC为一边的三角形共有( )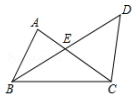 A、1个 B、2个 C、3个 D、4个3. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A、1个 B、2个 C、3个 D、4个3. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )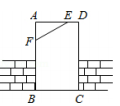 A、两点之间的线段最短 B、两点确定一条直线 C、三角形具有稳定性 D、长方形的四个角都是直角4. 若三角形三边长分别为2,x,3,且x为正整数,则这样的三角形个数为( )A、2 B、3 C、4 D、55. 若三角形三个内角度数比为2∶3∶4,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 将一副三角尺按如图所示的方式摆放,则 的大小为( )
A、两点之间的线段最短 B、两点确定一条直线 C、三角形具有稳定性 D、长方形的四个角都是直角4. 若三角形三边长分别为2,x,3,且x为正整数,则这样的三角形个数为( )A、2 B、3 C、4 D、55. 若三角形三个内角度数比为2∶3∶4,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 将一副三角尺按如图所示的方式摆放,则 的大小为( ) A、 B、 C、 D、7. 一个多边形的外角和是内角和的 , 这个多边形的边数是( )A、7 B、8 C、9 D、108. 下列说法正确的是( )A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、面积相等的两个三角形全等 D、全等三角形的面积一定相等9. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB= AC,现添加以下的哪个条件仍无法判定△ABE △ACD的是( )
A、 B、 C、 D、7. 一个多边形的外角和是内角和的 , 这个多边形的边数是( )A、7 B、8 C、9 D、108. 下列说法正确的是( )A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、面积相等的两个三角形全等 D、全等三角形的面积一定相等9. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB= AC,现添加以下的哪个条件仍无法判定△ABE △ACD的是( )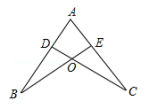 A、AD= AE B、∠B=∠C C、CD=BE D、∠ADC=∠AEB10. 如图,AABC 与MAEF中,AB= AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠AFE﹔②BF= DE,③∠BFE=∠BAE:④∠BFD=∠CAF.其中正确的结论有( )个
A、AD= AE B、∠B=∠C C、CD=BE D、∠ADC=∠AEB10. 如图,AABC 与MAEF中,AB= AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠AFE﹔②BF= DE,③∠BFE=∠BAE:④∠BFD=∠CAF.其中正确的结论有( )个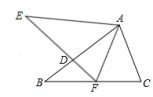 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本大题共7小题,每小题4分,共28分)
-
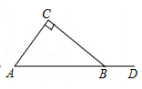
11. 已知△ABC中,∠A=30°,∠C=2∠B,则∠B=度.12. 如图,在Rt△ABC中,∠ACB=90°,∠A=50°,点D是AB延长线上的一点,则∠CBD的度数是度.
 13. 如图,△ACE △DBF,如果DA=12,CB=6,那么线段AB的长是.
13. 如图,△ACE △DBF,如果DA=12,CB=6,那么线段AB的长是.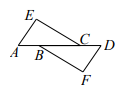 14. 如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE=cm.
14. 如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE=cm.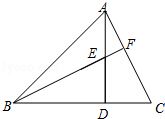 15. 如图,在△ABC中,AB=12,BC=10,AC=8,AD平分∠BAC交BC于点D,在AB上截取AE= AC,则 △ BDE的周长为.
15. 如图,在△ABC中,AB=12,BC=10,AC=8,AD平分∠BAC交BC于点D,在AB上截取AE= AC,则 △ BDE的周长为.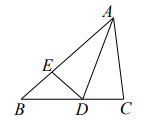 16. 如图,已知正五边形ABCDE,连接BE、AC交于点F,则∠AFE的大小为度。
16. 如图,已知正五边形ABCDE,连接BE、AC交于点F,则∠AFE的大小为度。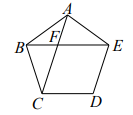 17. 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一动点,当△BDF为直角三角形时,则∠ADF的度数为.
17. 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一动点,当△BDF为直角三角形时,则∠ADF的度数为.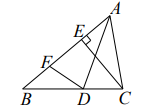
三、解答题(一)(本大题共3小题,每小题6分,共18分)
-
18. 如图,在△ABC中,BE是AC边上的高,DE//BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
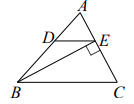 19. 如图:已知∠B=40°,∠C=59°,∠DEC=47°求∠F的度数。
19. 如图:已知∠B=40°,∠C=59°,∠DEC=47°求∠F的度数。 20. 一个多边形的内角和比它的外角和的2倍还大180度,求这个多边形的边数.
20. 一个多边形的内角和比它的外角和的2倍还大180度,求这个多边形的边数.四、解答题(二)(本大题共3小题,每小题8分,共24分)
-
21. 已知:如图,△ABC △ADEF ,AM 、DN分别是△ABC、△DEF的对应边上的高.
求证:AM=DN.
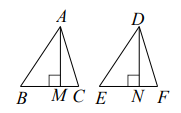 22. 均雄同学想知道一堵墙上点A的高度(AO⊥OD),但又没有直接测量的工具,于是设计了下面的方案,请你先补全方案,再说明理由.(1)、第一步:找一根长度大于OA的直杆,使直杆靠在墙上,且顶端与点A重合,记下直杆与地面的夹角二ABO ;
22. 均雄同学想知道一堵墙上点A的高度(AO⊥OD),但又没有直接测量的工具,于是设计了下面的方案,请你先补全方案,再说明理由.(1)、第一步:找一根长度大于OA的直杆,使直杆靠在墙上,且顶端与点A重合,记下直杆与地面的夹角二ABO ;第二步:使直杆顶端竖直缓慢下滑,直到∠=∠ .标记此时直杆的底端点D;
第三步:测量的长度,即为点A的高度.
(2)、说明理由: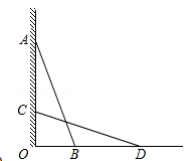 23. 已知:如图,CD=BE,DG上BC于点G,EF⊥BC于点F,且DG= EF .
23. 已知:如图,CD=BE,DG上BC于点G,EF⊥BC于点F,且DG= EF .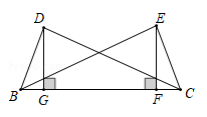 (1)、求证: △DGC △EFB ;(2)、连结BD,CE.求证:BD=CE.
(1)、求证: △DGC △EFB ;(2)、连结BD,CE.求证:BD=CE.五、解答题(三)(本大题共2小题,每小题10分,共20分)
-
24. 将一块直角三角板XYZ放置在AABC上,使得该三角板的两条直角边XY,XZ恰好分别经过点B,C.
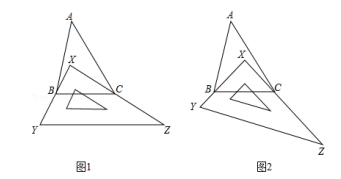 (1)、如图1,当∠A=45°时,∠ABC+∠ACB=度,∠ABX+∠ACX=度.(2)、如图2,改变直角三角板XYZ的位置,使该三角板的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明,若没有变化,请探究∠ABX+∠ACX与∠A的关系.25. 如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5 cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点Р运动结束时,点О运动随之结束).
(1)、如图1,当∠A=45°时,∠ABC+∠ACB=度,∠ABX+∠ACX=度.(2)、如图2,改变直角三角板XYZ的位置,使该三角板的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明,若没有变化,请探究∠ABX+∠ACX与∠A的关系.25. 如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5 cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点Р运动结束时,点О运动随之结束).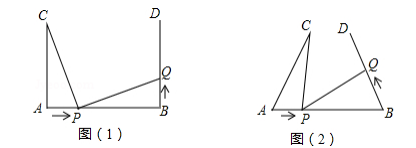 (1)、若点Q的运动速度与点Р的运动速度相等,当t =1s时,△ACP与△BPO是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点O的运动速度为x cm/s ,其它条件不变,当点P、O运动到何处时有△ACP与△BPO全等,求出相应的x的值.
(1)、若点Q的运动速度与点Р的运动速度相等,当t =1s时,△ACP与△BPO是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点O的运动速度为x cm/s ,其它条件不变,当点P、O运动到何处时有△ACP与△BPO全等,求出相应的x的值.