陕西省西安市莲湖区2021届九年级上学期数学第一次月考试卷

试卷更新日期：2020-11-17 类型：月考试卷

进入出卷网下载

一、单选题

1. 用公式法解一元二次方程 $3 x^{2} - 3 x = 1$ 时，化方程为一般式，当中的a、b、c依次为（）

A、3，-3，1 B、3，-3，-1 C、3，3，-1 D、3，3，1

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A D = D B$ ， $C D = 4$ ，则 $A B$ 的长度为（）

A、6 B、7 C、8 D、9

查看试题解析
3. 抛掷一枚质地均匀的硬币，“反面朝上”的概率为 $\frac{1}{2}$ ，那么抛掷一枚质地均匀的硬币100次，下列理解正确的是（）

A、每两次必有1次反面朝上 B、可能有50次反面朝上 C、必有50次反面朝上 D、不可能有100次反面朝上

查看试题解析
4. 菱形 $A B C D$ 的边长是 $5 cm$ ，一条对角线 $A C$ 的长是 $8 cm$ ，则此菱形的面积为（）

A、 $40 {cm}^{2}$ B、 $48 {cm}^{2}$ C、 $24 \sqrt{3} {cm}^{2}$ D、 $24 {cm}^{2}$

查看试题解析
5. 已知一元二次方程 $x^{2} - k x + 4 = 0$ 有两个相等的实数根，则k的值为（）

A、 $k = 4$ B、 $k = - 4$ C、 $k = \pm 4$ D、 $k = \pm 2$

查看试题解析
6. 如图，两个转盘分别自由转动一次（当指针恰好指在分界线上时重转），当停止转动时，两个转盘的指针都指向3的概率为（）

A、 $\frac{1}{16}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图，正方形 $A B C D$ 中，在 $B A$ 延长线上取一点E，使 $B E = B D$ ，连接 $D E$ ，则 $∠ E D A$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $30 °$ D、 $22.5 °$

查看试题解析
8. 已知一元二次方程 $x^{2} - 8 x + 12 = 0$ 的两根恰好是某等腰三角形的两边长，则该等腰三角形的底边长为（）

A、2 B、6 C、8 D、2或6

查看试题解析
9. 若 $x^{2} + m x + 20 = {(x - 4)}^{2} - n$ ，则 $m - n$ 的值是（）

A、-16 B、-12. C、-4 D、4

查看试题解析
10. 如图1，有一张长 $32 cm$ ，宽 $16 cm$ 的长方形硬纸片，裁去角上2个小正方形和2个小长方形（图中阴影部分）之后，恰好折成如图2所示的有盖纸盒.若纸盒的底面积是 $130 {cm}^{2}$ ，则纸盒的高为（）

A、 $2 cm$ B、 $2.5 cm$ C、 $3 cm$ D、 $4 cm$

查看试题解析

二、填空题

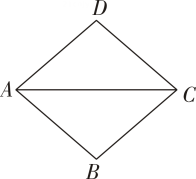
11. 如图，菱形ABCD中，∠ACD=40°，则∠ABC=°。

查看试题解析
12. 某学习小组全体同学都为本组其他人员送了一张新年贺卡，若全组共送贺卡156张，设这个小组的同学共有x人，可列方程：.

查看试题解析
13. 从2，-2，0三个数中任取两个不同的数作为点的坐标，则该点在坐标轴上的概率是.

查看试题解析
14. 有两个全等矩形纸条，长与宽分别为11和7，按如图所示的方式交叉叠放在一起，则重合部分构成的四边形 $B G D H$ 的周长为.

查看试题解析

三、解答题

15. 解方程： $x^{2} + 6 x - 16 = 0$

查看试题解析
16. 如图，四边形 $A B C D$ 是菱形，E、F是直线 $A C$ 上两点， $A F = C E$ .求证：四边形 $F B E D$ 是菱形.

查看试题解析
17. 在三角形 $A B C$ 中， $∠ C = 90 °$ ，请用尺规作图的方法，以 $A B$ 为对角线作一个矩形（保留作图痕迹，不写作法）.

查看试题解析
18. 若一元二次方程 $x^{2} - 2 x = 1$ 的两个实数根分别为 $x_{1}$ ， $x_{2}$ ，求 $(x_{1} - 1) (x_{2} - 1)$ 的值.

查看试题解析
19. 已知，如图，在 $R t △ A B C$ 中， $E$ 是两锐角平分线的交点， $E D ⊥ B C$ ， $E F ⊥ A C$ ，垂足分别为 $D$ ， $F$ ，求证：四边形 $C D E F$ 是正方形.

查看试题解析
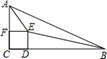20. 有四张正面分别标有数字1，2，3，4的不透明卡片，它们除数字外无其他差别，现将它们背面朝上洗匀.

(1)、随机抽取一张卡片，卡片上的数字是偶数的概率为.

(2)、随机抽取一张卡片，然后放回洗匀，再随机抽取一张卡片，请用列表或画树状图的方法，求两次抽取的卡片上的数字和等于5的概率.

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = 8 cm$ ， $B C = 10 cm$ ，点P由点A出发，沿 $A B$ 边以 $1cm/s$ 的速度向点B移动；点Q由点B出发，沿 $B C$ 边以 $2cm/s$ 的速度向点C移动.如果点P，Q分别从点A，B同时出发，问：

(1)、经过几秒后， $A P = C Q$ ？

(2)、经过几秒后， $△ P B Q$ 的面积等于 ${15cm}^{2}$ ？

查看试题解析
22. 一个不透明的口袋中装有若干个红球、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀.

(1)、从中任意摸出1个球，恰好摸到红球的概率是 $\frac{1}{2}$ ，则红球有个；

(2)、在（1）的条件下，从袋中任意摸出2个球，请用画树状图或列表的方法求摸出的球是一个红球和一个白球的概率.

查看试题解析
23. 如图，在矩形 $A B C D$ 中，点E在 $A D$ 上，且 $E C$ 平分 $∠ B E D$ .

(1)、求证： $B E = B C$ .

(2)、若 $B E = D C + D E$ ，求 $∠ B E C$ 的度数.

查看试题解析
24. 西安某特产商店将进价为每件20元的礼盒的售价确定为每件40元.

(1)、中秋期间，该商店进行降价促销活动，预备将原来售价进行两次降价，降价后该礼盒现价为32.4元.若该商品两次降价的降价率相同，求这个降价率；

(2)、经调查，该商品每降价2元，即可多销售100件.已知该商品售价40元时每月可销售500件，若该商店希望该商品每月能盈利10000元，且尽可能扩大销售量，则该商品在原售价的基础上应如何调整？

查看试题解析
25. 如图

(1)、如图1，在正方形 $A B C D$ 中， $A E$ 、 $D F$ 相交于点O且 $A E ⊥ D F$ .则 $A E$ 和 $D F$ 的数量关系为.

(2)、如图2，在正方形 $A B C D$ 中，E、F、G分别是边 $A D$ 、 $B C$ 、 $C D$ 上的点， $B G ⊥ E F$ ，垂足为H.求证： $E F = B G$ .

(3)、如图3，在正方形 $A B C D$ 中，E、F、M分别是边 $A D$ 、 $B C$ 、 $A B$ 上的点， $A E = 2$ ， $B F = 5$ ， $B M = 1$ ，将正方形沿 $E F$ 折叠，点M的对应点恰好与 $C D$ 边上的点N重合，求 $C N$ 的长度.

查看试题解析