辽宁省鞍山市台安县2021届九年级上学期数学10月月考试卷
试卷更新日期:2020-11-17 类型:月考试卷
一、单选题
-
1. 下列方程一定是一元二次方程的是( )A、 B、 C、 D、2. 若 是关于x的一元二次方程 的一个根,则 的值为( )A、2018 B、2020 C、2022 D、20243. 下列一元二次方程中有两个相等实数根的是( )A、2x2-6x+1=0 B、3x2-x-5=0 C、x2+x=0 D、x2-4x+4=04. 一元二次方程 配方后可化为( )A、 B、 C、 D、5. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、
 B、
B、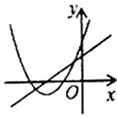 C、
C、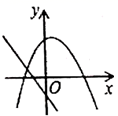 D、
D、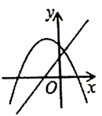 6. 下列关于二次函数y=2(x-3)2-1的说法,正确的是( )A、图象的对称轴是直线x=-3 B、图象向右平移3个单位则变为y=2(x﹣3)2﹣4 C、当x=3时,函数y有最大值﹣1 D、当x>3时,y随x的增大而增大7. 如图,要在一块长20米、宽15米的矩形地面上,修建了三条宽度相等的道路(其中两条路与宽平行,一条路与长平行)。若要使剩余部分的面积为208平方米,则道路的宽为( )米
6. 下列关于二次函数y=2(x-3)2-1的说法,正确的是( )A、图象的对称轴是直线x=-3 B、图象向右平移3个单位则变为y=2(x﹣3)2﹣4 C、当x=3时,函数y有最大值﹣1 D、当x>3时,y随x的增大而增大7. 如图,要在一块长20米、宽15米的矩形地面上,修建了三条宽度相等的道路(其中两条路与宽平行,一条路与长平行)。若要使剩余部分的面积为208平方米,则道路的宽为( )米 A、1 B、2 C、3 D、2.58. 已知函数 在 上的最大值是1,最小值是 ,则 的取值范围是( )A、 B、 C、 D、
A、1 B、2 C、3 D、2.58. 已知函数 在 上的最大值是1,最小值是 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
9. 一元二次方程 化成二次项系数为正数的一般形式后,它的常数项是.10. 如果函数 是关于 的二次函数,则 .11. 已知 ,那么 的值是.12. 在平面直角坐标系中,把一条抛物线先向上平移2个单位长度,再向左平移3个单位长度得到抛物线y=x2+4x+5,则原抛物线的解析式是.13. 若关于 的函数 与 轴仅有一个交点,则实数 的值为.14. 有一人患了流感,假如平均一个人传染了x个人,经过两轮感染后共有121人患了流感,依题意可列方程为.15. 已知两点 , 均在抛物线 上,点 是该抛物线的顶点,若 ,则 的取值范围是.16. 如图,抛物线 过点 ,且对称轴为直线 ,有下列结论:
① ;② ;③抛物线经过点 与点 ,则 ;④无论 取何值,抛物线都经过同一个点 ;⑤ ,其中所有正确的结论是.
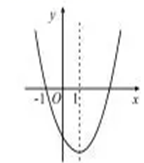
三、解答题
-
17. 解方程(1)、(2)、18. 已知关于x的方程 ,(1)、当 取何值时,方程有两个不相等的实数根?(2)、给 选取一个合适的整数,使方程有两个有理根,并求出这两个根.19. 如图,已知抛物线 经过 , 两点.
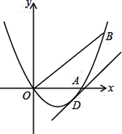 (1)、求抛物线的解析式;(2)、将直线 向下平移 个单位长度后,得到的直线与抛物线只有一个公共点 ,求 的值.20. 为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.(1)、求该学校为新增电脑投资的年平均增长率;(2)、从2016年到2018年,该中学三年为新增电脑共投资多少万元?21. 已知关于 的一元二次方程 的两个根分别为 , ,利用一元二次方程的求根公式可得: , ,利用上述结论来解答下列问题:(1)、已知 的两个根为 , ,则 , ;(2)、已知关于 的一元二次方程 有两个实数根 , ,若 ,求 的值.22. 已知如图,抛物线 与 轴正半轴交于点 ,与 轴交于点 ,点 在抛物线 的图象上,连接 , .
(1)、求抛物线的解析式;(2)、将直线 向下平移 个单位长度后,得到的直线与抛物线只有一个公共点 ,求 的值.20. 为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.(1)、求该学校为新增电脑投资的年平均增长率;(2)、从2016年到2018年,该中学三年为新增电脑共投资多少万元?21. 已知关于 的一元二次方程 的两个根分别为 , ,利用一元二次方程的求根公式可得: , ,利用上述结论来解答下列问题:(1)、已知 的两个根为 , ,则 , ;(2)、已知关于 的一元二次方程 有两个实数根 , ,若 ,求 的值.22. 已知如图,抛物线 与 轴正半轴交于点 ,与 轴交于点 ,点 在抛物线 的图象上,连接 , .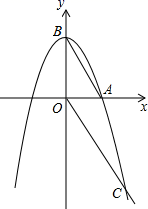 (1)、求抛物线 的函数表达式;(2)、若点 在 轴上,且 ,求所有满足条件的点 的坐标.23. 某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元.为了扩大销售,增加盈利,商场决定采取适当的降价措施,经调查发现,若每件降价1元,商场平均每天可多销售2件.(1)、若现在设每件衬衫降价 元,平均每天盈利为 元.求出 与 之间的函数关系式.(2)、当每件降价多少元时,商场平均每天盈利最多?此时,与降价前比较,每天销售这种商品可多获利多少元?(3)、若商场每天平均需盈利1200元,每件衬衫应降价多少元.24. 在高尔夫球训练中,运动员在距球洞 处击球,其飞行路线满足抛物线 ,其图象如图所示,其中球飞行高度为 ,球飞行的水平距离为 ,球落地时距球洞的水平距离为 .
(1)、求抛物线 的函数表达式;(2)、若点 在 轴上,且 ,求所有满足条件的点 的坐标.23. 某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元.为了扩大销售,增加盈利,商场决定采取适当的降价措施,经调查发现,若每件降价1元,商场平均每天可多销售2件.(1)、若现在设每件衬衫降价 元,平均每天盈利为 元.求出 与 之间的函数关系式.(2)、当每件降价多少元时,商场平均每天盈利最多?此时,与降价前比较,每天销售这种商品可多获利多少元?(3)、若商场每天平均需盈利1200元,每件衬衫应降价多少元.24. 在高尔夫球训练中,运动员在距球洞 处击球,其飞行路线满足抛物线 ,其图象如图所示,其中球飞行高度为 ,球飞行的水平距离为 ,球落地时距球洞的水平距离为 .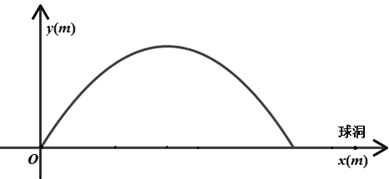 (1)、求 的值;(2)、若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;(3)、若球洞 处有一横放的 高的球网,球的飞行路线仍满足抛物线 ,要使球越过球网,又不越过球洞(刚好进洞),求 的取值范围.25. 2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数 (人)与时间 (分钟)的变化情况,数据如下表:(表中9-15表示 )
(1)、求 的值;(2)、若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;(3)、若球洞 处有一横放的 高的球网,球的飞行路线仍满足抛物线 ,要使球越过球网,又不越过球洞(刚好进洞),求 的取值范围.25. 2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数 (人)与时间 (分钟)的变化情况,数据如下表:(表中9-15表示 )时间 (分钟)
0
1
2
3
4
5
6
7
8
9
9~15
人数 (人)
0
170
320
450
560
650
720
770
800
810
810
(1)、根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出y与x之间的函数关系式;(2)、如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?(3)、在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?26. 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( , )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.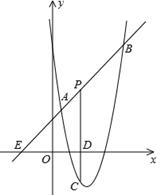 (1)、求抛物线的解析式;(2)、是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)、假若△PAC为直角三角形,直接写出点P坐标。
(1)、求抛物线的解析式;(2)、是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)、假若△PAC为直角三角形,直接写出点P坐标。