辽宁省沈阳市2020-2021学年八年级上学期数学第一次月考试卷(一)
试卷更新日期:2020-11-17 类型:月考试卷
一、单选题
-
1. 下列各数中,不是无理数的是( )A、 B、 C、 D、0.101001000……(相邻两个1之间0的个数依次加1)2. 下列各组数能作为直角三角形三边长的是( )A、 ,2, B、 , , C、7,24,25 D、12,15,203. 下列说法中正确的是( )A、0.09的平方根是0.3 B、 C、1的立方根是±1 D、0的立方根是04. 在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 设 ,则 的取值范围是( )A、 B、 C、 D、无法确定6. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、7. 下列各式,运算正确的是( )A、 B、 C、 D、8. 如图,在矩形 中, , ,边 在数轴上,以点 为圆心, 的长为半径作弧交数轴于点 ,则点 表示的数为( )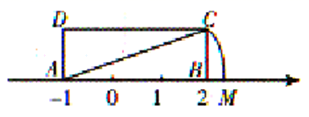 A、 B、 C、2 D、9. 如图,若每个小方格的面积为1,则图中以格点为端点且长度为 的线段有( )
A、 B、 C、2 D、9. 如图,若每个小方格的面积为1,则图中以格点为端点且长度为 的线段有( )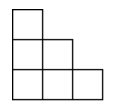 A、2条 B、3条 C、4条 D、5条10. 如图,一个底面直径为 cm,高为20cm的糖罐子,一只蚂蚁从A处沿着糖罐的表面爬行到B处,则蚂蚁爬行的最短距离是( )
A、2条 B、3条 C、4条 D、5条10. 如图,一个底面直径为 cm,高为20cm的糖罐子,一只蚂蚁从A处沿着糖罐的表面爬行到B处,则蚂蚁爬行的最短距离是( )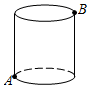 A、24cm B、10 cm C、25cm D、30cm11. 如图,斜靠在一面墙上的一根竹竿,它的顶端 距离地面的距离 为 ,底端 远离墙的距离 为 ,当它的顶端 下滑 时,底端 在地面上水平滑行的距离是.
A、24cm B、10 cm C、25cm D、30cm11. 如图,斜靠在一面墙上的一根竹竿,它的顶端 距离地面的距离 为 ,底端 远离墙的距离 为 ,当它的顶端 下滑 时,底端 在地面上水平滑行的距离是.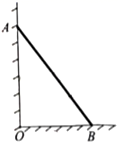 12. 有一个数值转换器,流程如图:
12. 有一个数值转换器,流程如图:
当输入x的值为64时,输出y的值是.
13. 如图,等边 的边 垂直于 轴,点 在 轴上已知点 ,则点 的坐标为.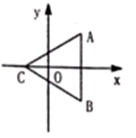
二、解答题
-
14. 计算: .15. 计算: .16. 计算: .17. 如图,在 中, , , ,点 从点 出发,以每秒 的速度向点 运动,连接 ,设运动时间为 秒 .
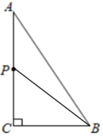 (1)、 ;(2)、当 时,求 的值.18. (阅读材料)
(1)、 ;(2)、当 时,求 的值.18. (阅读材料)我们已知 ,因此将 的分子、分母同时乘以“ ”,分母就由原来的无理数 就变成了有理数4.
即: .
这种当分母中含有二次根式时,通过恒等变形将分母变为有理式的过程称为分母有理化.
(理解应用)
(1)、化简求值: ;(2)、化简: .19. 如图,在 中, , ,点 是 边上一点, , .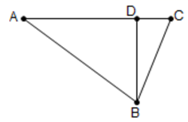 (1)、求证: ;(2)、若点 是 边上的动点,连接 ,求线段 的最小值.20. 如图是由边长为1的小正方形组成的 网格,格点 (顶点是网格线的交点的三角形)的顶点 , , 的坐标分别为(4,0),(3,5),(1,2).
(1)、求证: ;(2)、若点 是 边上的动点,连接 ,求线段 的最小值.20. 如图是由边长为1的小正方形组成的 网格,格点 (顶点是网格线的交点的三角形)的顶点 , , 的坐标分别为(4,0),(3,5),(1,2). (1)、在如图所示网格中,根据上述点的坐标建立适当的平面直角坐标系,标出原点 ;(2)、在(1)建立的平面直角坐标系中,
(1)、在如图所示网格中,根据上述点的坐标建立适当的平面直角坐标系,标出原点 ;(2)、在(1)建立的平面直角坐标系中,①画出 关于 轴对称的图形 ,点 , , 的对应点分别为 , , ,直接写出点 的坐标;
②若点 是 内部任意一点,直接写出点 关于 轴对称的对应点 的坐标.
21. 在等腰直角三角形 中, , .点 是射线 上一个动点,连接 ,以 为边在 的右侧作等腰直角三角形 , , .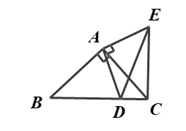
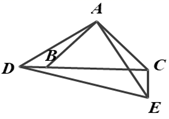 (1)、如图,当点 在线段 上时,
(1)、如图,当点 在线段 上时,①探究 与 的数量关系和位置关系,并说明理由;
②直接写出线段 , , 之间的数量关系;
(2)、如图,当点 在 的延长线上, 时,22. 如图,在平面直角坐标系内,四边形 的顶点 是坐标原点,点 在 轴正半轴上, .点 的坐标为(5,3),点 在 轴正半轴上, 轴,垂足为点 ,连接 ,点 是 轴正半轴上的一个动点,设点 的横坐标为 .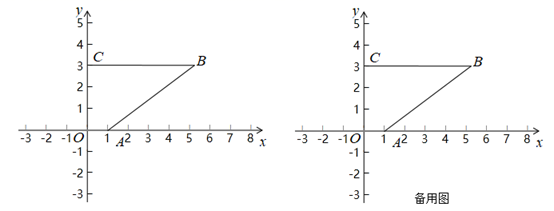 (1)、点 的坐标为.点 的坐标为;(2)、连接 ,设 的面积为 .
(1)、点 的坐标为.点 的坐标为;(2)、连接 ,设 的面积为 .①当 时,求 与 之间的函数关系式;
②当 时,直接写出 的值;
(3)、 点 是 边上一点,当 是等腰三角形,且点 与点 关于 对称时,直接写出点 的坐标.