江苏省无锡市东北塘2021届九年级上学期数学9月月考试卷

试卷更新日期：2020-11-16 类型：月考试卷

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} + 4 x + 5 = 0$ 的根的情况是（）

A、无实数根 B、有一个实根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
2. 已知△ABC∽△DEF，且相似比为1：2，则△ABC与△DEF的面积比为（）

A、1：4 B、4：1 C、1：2 D、2：1

查看试题解析
3. 已知⊙O与点P在同一平面内，如果⊙O的半径为5，线段OP的长为4，则点P（）

A、在⊙O上 B、在⊙O内 C、在⊙O外 D、在⊙O上或在⊙O内

查看试题解析
4.
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　　）

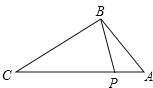A、∠ABP=∠C B、∠APB=∠ABC C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $\frac{A B}{B P} = \frac{A C}{C B}$

查看试题解析
5. 下列语句，错误的是（）

A、直径是弦 B、相等的圆心角所对的弧相等 C、弦的垂直平分线一定经过圆心 D、平分弧的半径垂直于弧所对的弦

查看试题解析
6. 某厂一月份生产产品150台，计划二、三月份共生产450台，设二、三月平均每月增长率为x，根据题意列出方程是（）

A、 $150 {(1 + x)}^{2} = 450$ B、 $150 (1 + x) + 150 {(1 + x)}^{2} = 450$ C、 $150 {(1 - x)}^{2} = 450$ D、 $150 {(1 + x)}^{2} = 600$

查看试题解析
7. 已知如图，点 C 是线段 AB 的黄金分割点（AC＞BC），则下列结论中正确的是（）

A、AB²＝AC²+BC² B、BC²＝AC•BA C、 $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{A C}{B C} = \frac{\sqrt{5} - 1}{2}$

查看试题解析
8. 在半径为 $1$ 的圆中，长度等于 $\sqrt{2}$ 的弦所对的弧的度数为（）

A、 $90^{\circ}$ B、 $145^{\circ}$ C、 $90^{\circ}$ 或 $270^{\circ}$ D、 $270^{\circ}$ 或 $145^{\circ}$

查看试题解析
9. A，B，C分别表示三个村庄， $A B = 1700$ 米， $B C = 800$ 米， $A C = 1500$ 米，某社区拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（）

A、AB的中点 B、BC的中点 C、AC的中点 D、 $∠ C$ 的平分线与AB的交点

查看试题解析
10. 如图，直角梯形ABCD中，∠BCD＝90°，AD∥BC，BC＝CD，E为梯形内一点，且∠BEC＝90°，将△BEC绕C点旋转90°使BC与DC重合，得到△DCF，连EF交CD于M.已知BC＝5，CF＝3，则DM：MC的值为（）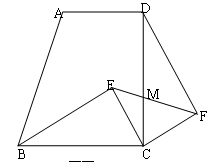

A、5：3 B、3：5 C、4：3 D、3：4

查看试题解析

二、填空题

11. 一元二次方程x²＝2x的解为.

查看试题解析
12. 一元二次方程x²－6x＋5＝0的两根分别是x₁、x₂ ，则x₁·x₂的值是.

查看试题解析
13. 在比例尺为1：8000的南京市城区地图上，太平南路的长度约为25 cm，它的实际长度约为m.

查看试题解析
14. 如图，四边形ABCD为 $⊙ O$ 的内接四边形，已知 $∠ BOD = 110^{\circ}$ ，则 $∠ BCD$ 的度数为.

查看试题解析
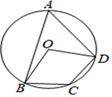15. 如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB的高度为36cm，那么它在暗盒中所成的像CD的高度应为cm.

查看试题解析
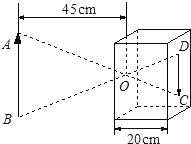16. 如图，已知点C是⊙O的直径AB上的一点，过点C作弦DE，使CD=CO.若 $\overset{⌢}{A D}$ 的度数为35°，则 $\overset{⌢}{B E}$ 的度数是.

查看试题解析
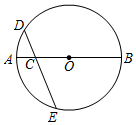17. 若m，n是方程x²＋x－1=0的两个实数根，则m²＋2m＋n的值为.

查看试题解析
18. 如图，在 Rt△ ABC中，∠C=90°，AB=10，AC=8，点D在斜边AB上，把△ACD沿直线CD翻折，使得点A落在平面内的A′处，当A′D平行于Rt△ABC的直角边时，则AD长为.

查看试题解析

三、解答题

19. 解方程：

(1)、 ${(2 x + 1)}^{2} = 9$ ；

(2)、2x²﹣4x＝1（配方法）；

(3)、 $2 x^{2} - 5 x + 1 = 0$ ；

(4)、 ${(x - 3)}^{2} - 4 x (3 - x) = 0$

查看试题解析
20. 已知关于x的方程 $x^{2} - 2 x + m - 1 = 0$ .

(1)、若方程有两个不相等的实数根，求m的取值范围；

(2)、若方程有一个实数根是5，求此方程的另一个根.

查看试题解析
21. 已知：如图，AB为⊙O的直径，OD∥AC.求证：点D平分 $\overset{⌢}{BC}$ .

查看试题解析
22. 如图，正方形ABCD中，M为BC上一点， $ME ⊥ AM$ ，ME交AD的延长线于点E.

(1)、求证： $△ ABM$ ∽ $△ EMA$ ；

(2)、若 $AB = 4$ ， $BM = 2$ ，求DE的长.

查看试题解析
23. 如图，在⊙O中，弦AB的长为10，半径OD⊥AB，垂足为C，E为⊙O上任意一点，连接DE、BE.

(1)、若∠AOD＝50°，求∠DEB的度数；

(2)、若OC＝2CD，求CD的长.

查看试题解析
24. 如图，在边长为1的正方形网格中，有一格点△ABC，已知A、B、C三点的坐标分别是A（1，0）、B（2，－1）、C（3，1）.

①请在网格图形中画出平面直角坐标系；

②以原点O为位似中心，将△ABC放大2倍，画出放大后的△A′B′C′；

③写出△A′B′C′各顶点的坐标，

④写出△A′B′C′的重心坐标.

查看试题解析
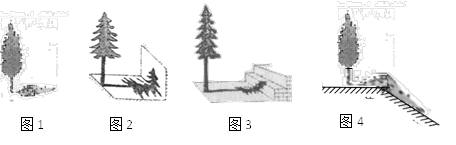
25. 商场销售服装，平均每天可售出20件，每件盈利40元，为扩大销售量，减少库存，该商场决定采取适当的降价措施，经调查发现，一件衣服降价1元，每天可多售出2件.

(1)、设每件降价x元，可以销售出件.（用x的的代数式表示）

(2)、若商场每天要盈利1200元，同时尽量减少库存，每件应降价多少元？

(3)、每件降价多少元时，商场每天盈利达到最大？最大盈利是多少元？

查看试题解析
26. 阅读以下文字并解答问题：在“物体的高度”活动中，某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下，他们分别做了以下工作：
小芳：测得一根长为1米的竹竿的影长为0.8米，甲树的影长为4.08米（如图1）.

小华：发现乙树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图2），墙壁上的影长为1.2米，落在地面上的影长为2.4米.

小丽：测量的丙树的影子除落在地面上外，还有一部分落在教学楼的第一级台阶上（如图3），测得此影子长为0.2米，一级台阶高为0.3米，落在地面上的影长为4.4米.

小明：测得丁树落在地面上的影长为2.4米，落在坡面上影长为3.2米（如图4）.身高是1.6m的小明站在坡面上，影子也都落坡面上，小芳测得他的影长为2m.

(1)、在横线上直接填写甲树的高度为米.

(2)、求出乙树的高度（画出示意图）.

(3)、请选择丙树的高度为（）

A、6.5米 B、5.75米 C、6.05米 D、7.25米

(4)、你能计算出丁树的高度吗？试试看.

查看试题解析
27. （发现问题）爱好数学的小明在做作业时碰到这样的一道题目：
如图①，点O为坐标原点，⊙O的半径为1，点A（2，0）.动点B在⊙O上，连结AB，作等边△ABC（A，B，C为顺时针顺序），求OC的最大值

（解决问题）小明经过多次的尝试与探索，终于得到解题思路：在图①中，连接OB，以OB为边在OB的左侧作等边三角形BOE，连接AE.

(1)、请你找出图中与OC相等的线段，并说明理由；

(2)、求线段OC的最大值.

(3)、如图②，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA＝2，PM＝PB，∠BPM＝90°，求线段AM长的最大值及此时点P的坐标.

(4)、如图③，BC＝4 $\sqrt{2}$ ，点D是以BC为直径的半圆上不同于B、C的一个动点，以BD为边作等边△ABD，请直接写出AC的最值.

查看试题解析