江西省宜春市丰城市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 化简 ${(- 1)}^{2020}$ 的值是（）

A、1 B、 $- 2020$ C、2020 D、 $- 1$

查看试题解析
2. 如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能符合题意解释这一现象的数学知识是（）

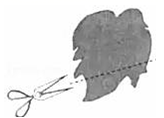A、垂线段最短 B、经过一点有无数条直线 C、两点之间，线段最短 D、经过两点，有且仅有一条直线

查看试题解析
3. 有理数a，b在数轴上对应点的位置如图所示，下列说法中正确的是（　　）

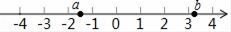A、a＞b B、 $a > \frac{1}{b}$ C、a＜﹣b D、|a|＜|b|

查看试题解析
4. 下列计算正确的是（　　）

A、 $5 a^{2} b - 4 a^{2} b = a^{2} b$ B、 $a + b = a b$ C、 $6 a^{3} - 2 a^{3} = 4$ D、 $2 b^{2} + 3 b^{3} = 5 b^{5}$

查看试题解析
5. 拒绝“餐桌浪费”，刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克，这个数据用科学记数法表示为（）

A、0.5×10¹¹千克 B、50×10⁹千克 C、5×10⁹千克 D、5×10¹⁰千克

查看试题解析
6. 某商场购进一批服装，又恰巧碰到双十一的促销活动，商场决定将这批服装按标价的五折销售，若打折后每件服装可获纯利润60元，其利润率为10%；若双十一过后，该商场按这批服装的标价打八折出售，那么获得的纯利润是（）

A、264元 B、396元 C、456元 D、660元

查看试题解析

二、填空题

7. 如果一个角与它的余角之比为1：2，那么这个角为度．

查看试题解析
8. 若 $x^{2} - 3 x = 1$ ，则 $2 x^{2} - 6 x + 2019$ 的值是

查看试题解析
9. 古代名著《算学启蒙》中有一题：良马日行二百四十里．驽马日行一百五十里．驽马先行一十二日，问良马几何追及之．意思是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可追上慢马？若设快马 $x$ 天可追上慢马，则由题意，可列方程为．

查看试题解析
10. 对于有理数a、b ，定义a*b＝3a+2b ，化简x*（x﹣y）＝．

查看试题解析
11. 如图，将一副直角三角扳叠在一起，使直角顶点重合于O点，则∠AOB+∠DOC=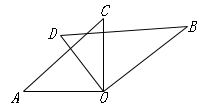

查看试题解析
12. 已知平面内有A、B、C、D四点，过其中的两点画一条直线，一共可以画条直线．

查看试题解析

三、解答题

13.

(1)、计算：-3- 2 +（-4）-（-1）

(2)、化简： $(a - 2 b) - (2 b - 3 a) - 2 (a - 3 b)$

查看试题解析
14. 解方程： $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$ ．

查看试题解析
15. 如图，已知线段AB=10cm ，延长AB到C ，使AC=18cm ， D是AB的中点，E是AC的中点，求DE的长.

查看试题解析
16. 如图，以直线AB上的点O为端点作射线OC、OD ，满足∠AOC＝54°，∠BOD＝ $\frac{1}{3}$ ∠BOC ，求∠BOD的度数．

查看试题解析
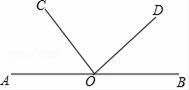17. 已知正方体的展开图如图所示，如果正方体的六个面分别用字母A，B，C，D，E，F表示，当各面上的数分别与它对面的数互为相反数，且满足B=1，C=﹣a²﹣2a+1，D=﹣1，E=3a+4，F=2﹣a时，求A面表示的数值．

查看试题解析
18. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - 4 (- a b^{2} + 3 a^{2} b)$ ，且 $| a + 2 | + {(b - 3)}^{2} = 0$ .

查看试题解析
19. 如图，直线AB与CD相交于O ， OE是∠AOC的平分线，OF⊥CD ， OG⊥OE ， ∠BOD=52°．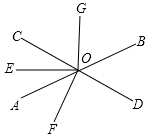

(1)、求∠AOC ， ∠AOF的度数；

(2)、求∠EOF与∠BOG是否相等？请说明理由．

查看试题解析
20. 已知点O为直线AB上一点，将直角三角板MON的直角顶点放在点O处，并在∠MON内部作射线OC ．

(1)、将三角板放置到如图所示位置，使OC恰好平分∠MOB ，且∠BON＝2∠NOC ，求∠AOM的度数；

(2)、若仍将三角板按照如图所示的方式放置，仅满足OC平分∠MOB ，试猜想∠AOM与∠NOC之间的数量关系，并说明理由．

查看试题解析

21. 为庆祝“元旦”，光明学校统一组织合唱比赛，七、八年级共92人（其中七年级的人数多于八年级的人数，且七年级的人数不足90人）准备统一购买服装参加比赛.下面是某服装厂给出服装的价格表：

购买服装的套数	1套至45套	46套至90套	91套以上（含91套）
每套服装的价格	60元	50元	40元
购买服装的套数	1套至45套	46套至90套	91套以上（含91套）
每套服装的价格	60元	50元	40元

(1)、如果两个年级分别单独购买服装一共应付5000元，求七、八年级各有多少学生参加合唱比赛；

(2)、如果七年级参加合唱比赛的学生中，有10名同学抽调去参加绘画比赛，不能参加合唱比赛，请你为两个年级设计一种最省钱的购买服装方案.

查看试题解析

22. 已知数轴上三点M ， O ， N对应的数分别为－1，0，3，点P为数轴上任意一点，其对应的数为x ．

(1)、MN的长为；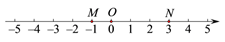

(2)、如果点P到点M、点N的距离相等，那么x的值是；

(3)、数轴上是否存在点P ，使点P到点M、点N的距离之和是8？若存在，直接写出x的值；若不存在，请说明理由．

(4)、如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动. 设t分钟时点P到点M、点N的距离相等，求t的值.

查看试题解析