江西省南昌市东湖区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，棱锥是（）

A、 B、 C、 D、

查看试题解析
2. 如图，正方体的平面展开图，每个面上都标有一个汉字，与“中”字相对的面上的字为（　　）

A、宜 B、居 C、城 D、市

查看试题解析
3. 某市为提倡节约用水，采取分段收费．若每户每月用水不超过20m³ ，每立方米收费2元；若用水超过20m³ ，超过部分每立方米加收1元．小明家5月份交水费64元，则他家该月用水（）m³ ．

A、38 B、34 C、28 D、44

查看试题解析
4. 如图，与∠1是同旁内角的是（）

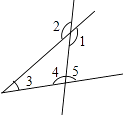A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
5. 若关于x的方程（m﹣2）x^|m|^﹣¹+3=0是一元一次方程，则m值为（　　）

A、﹣2 B、2 C、﹣3 D、3

查看试题解析
6. 《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四．问人数，物价各几何？译文为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问共有多少人？这个物品的价格是多少？设这个物品的价格是x元，则可列方程为（）

A、8x+3=7x+4 B、8x﹣3=7x+4 C、 $\frac{x - 3}{8} = \frac{x + 4}{7}$ D、 $\frac{x + 3}{8} = \frac{x - 4}{7}$

查看试题解析

二、填空题

7. 若代数式 $2 x^{2} - 4 x - 5$ 的值为7，则 $x^{2} - 2 x - 2$ 的值为 .

查看试题解析
8. 计算：
①33°52′+21°54′=；

②18.18°=°′″．

查看试题解析
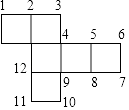
9.
如图是一个正方体纸盒的展开图，当折成纸盒时，与数11重合的数是．

查看试题解析
10. 一列方程如下排列：
$\frac{x}{4}$ + $\frac{x - 1}{2}$ =1的解是x=2，
$\frac{x}{6}$ + $\frac{x - 2}{2}$ =1的解是x=3，
$\frac{x}{8}$ + $\frac{x - 3}{2}$ =1的解是x=4，
…
根据观察得到的规律，写出其中解是x=6的方程：．

查看试题解析
11. 一个两位数，个位数字与十位数字的和是9，如果将个位数字与十位数字对调后所得的新数比原数大9，则原来的两位数是。

查看试题解析
12. 从点O引出三条射线OA ， OB ， OC ，已知∠AOB=30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC= ．

查看试题解析

三、解答题

13.

(1)、计算：11°23′26″×3；

(2)、解方程： $\frac{1 - 2 x}{3} = \frac{3 x + 17}{7} - 1$ ．

查看试题解析
14. 已知点A、B、C在同一条直线上，且AC=5cm，BC=3cm，点M、N分别是AC、BC的中点．

(1)、画出正确的图形；

(2)、依据（1）的图形，求线段MN的长．

查看试题解析
15. 如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠AOD：∠BOD＝2：1

(1)、求∠DOE的度数；

(2)、求∠AOF的度数．

查看试题解析
16. 已知关于x的方程3[x-2（x- $\frac{a}{3}$ ）]＝4x和 $\frac{3 x + a}{4} - \frac{1 - 5 x}{8}$ ＝1有相同的解，求这个解．

查看试题解析
17. 机械厂加工车间有85名工人，平均每人每天加工大齿轮16个或小齿轮10个，2个大齿轮和3个小齿轮配成一套，问需分别安排多少名工人加工大、小齿轮，才能使每
天加工的大小齿轮刚好配套？

查看试题解析
18. 若关于x的方程 $\frac{1}{2}$ mx- $\frac{5}{3}$ ＝ $\frac{1}{2}$ （x- $\frac{4}{3}$ ）有负整数解，求整数m的值．

查看试题解析
19. 有一叠卡片，自上而下按规律分别标有6，12，18，24，30，…等数字．

(1)、你能发现这些卡片上的数字有什么规律吗？请将它用一个含有n（n≥1）的式子表示出来；

(2)、小明从中抽取相邻的3张，发现其和是342，你能知道他抽出的卡片是哪三张吗？

(3)、你能拿出相邻的3张卡片，使得这些卡片上的数字之和是86吗？为什么？

查看试题解析
20. 某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的 $\frac{1}{2}$ 倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价﹣进价）

甲

乙

进价（元/件）

22

30

售价（元/件）

29

40

(1)、该超市购进甲、乙两种商品各多少件？

(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

(3)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙商品是按原价打几折销售？

查看试题解析
21. 如图1，长方形OABC的边OA在数轴上，O为原点，长方形OABC的面积为12，边OC长为3．

(1)、数轴上点A表示的数为；

(2)、将长方形OABC沿数轴水平移动，移动后的长方形记为O′A′B′C′，移动后的长方形O′A′B′C′与原长方形OABC重叠部分（如图2中阴影部分）的面积记为S ．
①当S恰好等于原长方形OABC面积的一半时，数轴上点A′表示的数是多少？

②设点A移动的距离AA′＝x ，当S＝4时，求x的值．

查看试题解析
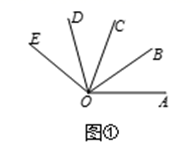
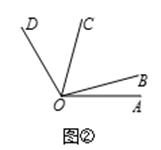22. 若 $∠ α$ 的度数是 $∠ β$ 的度数的k倍，则规定 $∠ α$ 是 $∠ β$ 的k倍角.

(1)、若∠M=21°17'，则∠M的5倍角的度数为；

(2)、如图1，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOC=∠COE，请直接写出图中∠AOB的所有3倍角；

(3)、如图2，若∠AOC是∠AOB的5倍角，∠COD是∠AOB的3倍角，且∠AOC和∠BOD互为补角，求∠AOD的度数.

查看试题解析
23. 已知：如图1，点M是线段AB上一定点，AB＝12cm ， C、D两点分别从M、B出发以1cm/s、2cm/s的速度沿直线BA向左运动，运动方向如箭头所示（C在线段AM上，D在线段BM上）

(1)、若AM＝4cm ，当点C、D运动了2s ，此时AC＝， DM＝；（直接填空）

(2)、当点C、D运动了2s ，求AC+MD的值．

(3)、若点C、D运动时，总有MD＝2AC ，则AM＝（填空）

(4)、在（3）的条件下，N是直线AB上一点，且AN﹣BN＝MN ，求 $\frac{M N}{A B}$ 的值．

查看试题解析

	甲	乙
进价（元/件）	22	30
售价（元/件）	29	40