江西省吉安市吉州区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 2019的相反数是（）

A、2019 B、-2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 用一个平面去截圆柱体，则截面形状不可能是（）

A、正方形 B、三角形 C、长方形 D、圆

查看试题解析
3. $2019$ 年年底通车的吉安西站，它的修建可以促进原中央苏区的振兴发展和吉泰走廊的建设发展，预计总投资约 $16.5$ 亿元， $16.5$ 亿用科学记数法可表示为（）

A、 $1.65 \times 10^{9}$ B、 $1.65 \times 10^{10}$ C、 $1.65 \times 10^{11}$ D、 $1.65 \times 10^{12}$

查看试题解析
4. 下列调查中，最适合采用普查方式的是（）

A、调查某批次烟花爆竹的燃放效果 B、调查奶茶市场上奶茶的质量情况 C、调查某班级的每一个同学所穿鞋子的尺码情况 D、调查吉安市中学生的心理健康现状

查看试题解析
5. 如果 $\frac{1}{3} x^{a + 2} y^{3}$ 与 $- 3 x^{3} y^{2 b - 1}$ 是同类项，那么a、b的值分别是（）

A、 ${\begin{array}{l} a = 1 \\ b = 1 \end{array}$ B、 ${\begin{array}{l} a = 0 \\ b = 2 \end{array}$ C、 ${\begin{array}{l} a = 2 \\ b = 1 \end{array}$ D、 ${\begin{array}{l} a = 1 \\ b = 2 \end{array}$

查看试题解析
6. 下列语句正确的个数是（）
①两条射线组成的图形叫做角

②反向延长线段 $A B$ 得到射线 $B A$

③延长射线 $O A$ 到点C

④若 $A B = B C$ ，则点B是 $A C$ 中点

⑤连接两点的线段叫做两点间的距离

⑥两点之间线段最短

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题

7. 当 $a =$ 时，关于x的方程 $3 x - 2 a + 5 = 0$ 的解是 $x = 1$

查看试题解析
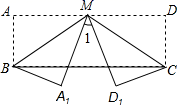
8. 上午8点30分，时钟的时针和分针所构成的锐角度数为

查看试题解析
9. 过一个多边形的一个顶点的所有对角线把多边形分成 $2019$ 个三角形，则这个多边形的边数为．

查看试题解析
10. 如图所示，在矩形纸片 $A B C D$ 中，点M为 $A D$ 边的中点，将纸片沿 $B M$ ， $C M$ 折叠，使点A落在 $A_{1}$ 处，点 $D$ 落在 $D_{1}$ 处，若 $∠ 1 = 30 °$ ，则 $∠ B M C$ 的度数为．

查看试题解析
11. $20$ 个工人生产螺栓和螺母，已知一个工人每天生产 $3$ 个螺栓或 $4$ 个螺母，且一个螺栓配 $2$ 个螺母，如何分配工人使生产的螺栓与螺母恰好配成套．如果设生产螺栓的工人数为x个，根据题意可列方程为：．

查看试题解析
12. 已知 $| m | = 3$ ， $| n | = 5$ ，则 $m - n =$ ．

查看试题解析
13. 把下列各数填入相应的大括号内
$- 13.5$ ， $2$ ， $0$ ， $3.14$ ， $- 27$ ， $- 15 %$ ， $- 1$ ， $\frac{22}{7}$

负数集合 ${$ $\dots$ $}$

整数集合 ${$ $\dots$ $}$

分数集合 ${$ $\dots$ $}$

查看试题解析

三、解答题

14.

(1)、 $- 12 - {(- 2)}^{3} \div \frac{4}{5} + 3 \times | 1 - {(- 2)}^{2} |$

(2)、解方程： $4 x - 3 (5 - x) = 6$

查看试题解析
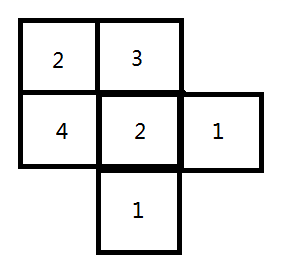
15. 从上面看由一些大小相同的小立方体组成的简单几何体，得到的图形如图所示，小正方形中的数字表示在该位置的小立方体的个数，请你画出这个几何体从左面和正面看到的图形．

查看试题解析
16. 先化简，再求值： $3 x^{2} y - [2 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y)] + 3 x y^{2} - x y ，$ 其中 $x = 3 ， y = - \frac{1}{3} .$

查看试题解析
17. 如图，点C在线段AB上，线段AC=8cm，BC=4cm，点M、N分别是AC、BC的中点，求：

(1)、线段MN的长度．

(2)、根据（1）的计算过程和结果，设AC+BC=a，其它条件不变，你能猜测出MN的长度吗？请证明你的猜测．

查看试题解析

18. 为有效治理污染，改善生态环境，山西太原成为国内首个实现纯电动出租车的城市，绿色环保的电动出租车受到市民的广泛欢迎，给市民的生活带来了很大的方便，下表是行驶路程在15公里以内时普通燃油出租车和纯电动出租车的运营价格：

车型	起步公里数	起步价格	超出起步公里数后的单价
普通燃油型	3	13元	2.3元/公里
纯电动型	3	8元	2元/公里

张先生每天从家打出租车去单位上班（路程在15公里以内），结果发现，正常情况下乘坐纯电动出租车比乘坐燃油出租车平均每公里节省0.8元，求张先生家到单位的路程．

查看试题解析

19. 为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每符合题意听写出一个汉字得1分，本次决赛，学生成绩为x（分），且

50 \leq x < 100

，将其按分数段分为五组，绘制出以下不完整表格：

组别	成绩x（分）	频数（人数）	频率
一	$50 \leq x < 60$	2	0.04
二	$60 \leq x < 70$	10	0.2
三	$70 \leq x < 80$	14	b
四	$80 \leq x < 90$	a	0.32
五	$90 \leq x < 100$	8	0.16

请根据表格提供的信息，解答以下问题：

(1)、本次决赛共有名学生参加；

(2)、直接写出表中a= ， b=；

(3)、请补全下面相应的频数分布直方图；

(4)、若决赛成绩不低于80分为优秀，则本次大赛的优秀率为．

查看试题解析

20. 将一个正方体的表面涂上颜色．如图把正方体的棱

2

等分，然后沿等分线把正方体切开，能够得到

8

个小正方体，通过观察我们可以发现

8

个小正方体全是

3

个面涂有颜色的．如果把正方体的棱三等分，然后沿等分线把正方体切开，能够得到

27

个小正方体，通过观察我们可以发现这些小正方体中有

8

个是

3

个面涂有颜色的，有

12

个是

2

个面涂有颜色的，有

6

个是

1

个面涂有颜色的，还有

1

个各个面都没有涂色．

(1)、如果把正方体的棱

4

等分，所得小正方体表面涂色情况如何呢？把正方体的棱

n

等分呢？（请填写下表）：

棱等分数	4等分	n等分
$3$ 面涂色的正方体	个	个
$2$ 面涂色的正方体	个	个
$1$ 面涂色的正方体	个	个
各个面都无涂色的正方体	个	个

(2)、请直接写出将棱

7

等分时只有一个面涂色的小正方体的个数．

查看试题解析

21. 已知，A、B在数轴上对应的数分别用a、b表示，且 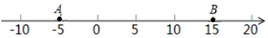${(a + 5)}^{2} + | b - 15 | = 0$ ．

(1)、数轴上点A表示的数是，点B表示的数是；

(2)、若一动点P从点A出发，以 $3$ 个单位长度秒速度由A向B运动；动点Q从原点O出发，以 $1$ 个单位长度l秒速度向B运动，点P、Q同时出发，点Q运动到B点时两点同时停止．设点Q运动时间为t秒．
若P从A到B运动，则P点表示的数为， Q点表示的数为（用含t的式子表示）

(3)、当t为何值时，点P与点Q之间的距离为 $2$ 个单位长度．

查看试题解析

22. 将正整数

1

至

2019

按照一定规律排成下表：

$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
$9$	$10$	$11$	$12$	$13$	$14$	$15$	$16$
$17$	$18$	$19$	$20$	$21$	$22$	$23$	$24$
$25$	$26$	$27$	$28$	$29$	$30$	$31$	$32$
……

记 $a_{i j}$ 表示第i行第j个数，如 $a_{14} = 4$ 表示第 $1$ 行第 $4$ 个数是 $4$ ．

(1)、直接写出

a_{42} =

，

a_{53} =

；

(2)、①如果

a_{i j} = 2019

，那么

i =

，

j =

；②用i，j表示

a_{i j} =

；

(3)、将表格中的

5

个阴影格子看成一个整体并平移，所覆盖的

5

个数之和能否等于

2027

．若能，求出这

5

个数中的最小数，若不能说明理由．

查看试题解析

23. 如图 1，射线 OC在∠AOB的内部，图中共有 3个角：∠AOB、∠AOC 和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线 OC是∠AOB的奇妙线.

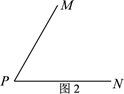
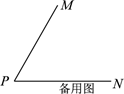(1)、一个角的角平分线这个角的奇妙线.（填是或不是）；

(2)、如图 2，若∠MPN＝60°，射线 PQ绕点 P从 PN位置开始，以每秒 10°的速度逆时针旋转，当∠QPN首次等于 180°时停止旋转，设旋转的时间为 t（s）.
①当 t为何值时，射线 PM是∠QPN 的奇妙线？

②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转，并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.

查看试题解析