江西省抚州市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2020的倒数是（）

A、﹣2020 B、﹣ $\frac{1}{2020}$ C、2020 D、 $\frac{1}{2020}$

查看试题解析
2. 下列运算正确的是（）

A、 $2 x + 2 y = 4 x y$ B、 $5 x + x = 5 x^{2}$ C、 $- 3 m n + n m = - 2 m n$ D、 $8 a^{2} b - 7 b a^{2} = 1$

查看试题解析
3. 若数a，b在数轴上的位置如图示，则（）

A、a+b＞0 B、ab＞0 C、a﹣b＞0 D、﹣a﹣b＞0

查看试题解析
4. 下列叙述错误的选项是（）

A、单项式 $- a b^{2}$ 的系数是-1，次数是3次 B、一个棱柱有7个面，则这个棱柱有10个顶点 C、把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线 D、钟面上3点30分，时针与分针的夹角为90度

查看试题解析
5. 如图，已知线段AB的长度为a，CD的长度为b，则图中所有线段的长度和为（）

A、3a+b B、3a-b C、a+3b D、2a+2b

查看试题解析
6. 如下表，从左到右在每个小格子中填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，若前m个格子中所填整数之和是2020，则m的值为（）

A、202 B、303 C、606 D、909

查看试题解析

二、填空题

7. 已知单项式 $3 a^{m} b^{2}$ 与 $- 2 a^{4} b^{n - 1}$ 的和是单项式，则m+n= ．

查看试题解析
8. 首届中国国际进口博览会于2018年11月5日至10日在上海国家会展中心举行，据新华社电，此次进博会交易采购成果丰硕，按一年计累计，意向成交410000000元，其中410000000用科学记数法表示为．

查看试题解析
9. 某件商品的标价是110元，按标价的八折销售时，仍可获利10%，则这件商品每件的进价为元．

查看试题解析
10. 定义 $a \times b = a^{3} - b^{2}$ ，则 $(2 ※ 3) ※ (- 1) =$ ．

查看试题解析
11. 如图所示，数轴上点A，点B，点C分别表示有理数a，b，c，O为原点，化简： $| b | + | a - c | - | b - c | =$ ．

查看试题解析
12. 射线 $O A$ ， $O B$ ， $O C$ ， $O D$ 是同一平面内互不重合的四条射线， $∠ A O B = 60 °$ ， $∠ A O D = 40 °$ ， $∠ A O B = 3 ∠ B O C$ ，则 $∠ C O D$ 的度数为．

查看试题解析

三、解答题

13. 计算：

(1)、 $2019 - (- 20) - | - 19 |$

(2)、 $- 1^{2020} - {(- 2)}^{5} \div {(- 4)}^{2} - 3^{3} \times \frac{1}{9}$ ．

查看试题解析
14. 先化简，再求值：若 ${(x + 2)}^{2} + | y - 1 | = 0$ ，求 $4 x y - 2 (2 x^{2} + 5 x y - y^{3}) + 2 (x^{2} + 3 x y)$ 的值．

查看试题解析
15. 解方程： $1 - \frac{3 x + 1}{2} = \frac{5 x + 13}{4}$ ．

查看试题解析
16. 乐乐和同学们研究“从三个方向看物体的形状”.

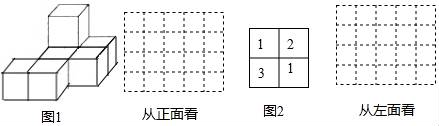(1)、图1中几何体是由几个相同的小立方块搭成的，请画出从正面看到的该几何体的形状图；

(2)、图2是由几个相同的小立方块组成的几何体从上面看到的形状图，小正方形中的数字表示该位置上小立方块的个数，请画出这个几何体从左面看到的形状图.

查看试题解析
17. 观察下列各式
$- 1 \times \frac{1}{2} = - 1 + \frac{1}{2}$ ；

$- \frac{1}{2} \times \frac{1}{3} = - \frac{1}{2} + \frac{1}{3}$ ；

$- \frac{1}{3} \times \frac{1}{4} = - \frac{1}{3} + \frac{1}{4}$ ；

……

(1)、你发现的规律是：（用正整数n表示规律）

(2)、应用规律计算： $(- 1 \times \frac{1}{2}) + (- \frac{1}{2} \times \frac{1}{3}) + (- \frac{1}{3} \times \frac{1}{4}) + \dots \dots + (- \frac{1}{2019} \times \frac{1}{2020})$

查看试题解析
18. 随着科技的进步和网络资源的丰富，在线学习已经成为更多人的自主学习选择．某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论．为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图．

(1)、求本次调查的学生总人数，并补全条形统计图；

(2)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

(3)、该校共有学生3000人，请你估计该校对在线阅读最感兴趣的学生人数．

查看试题解析
19. 用如图1所示的曲尺形框框（有三个方向），可以套住图2日历中的三个数，设被框住的三个数中（第一个框框住的最大的数为a、第二个框框住的最大的数为b、第三个框框住的最大的数为c）

(1)、第一个框框住的三个数的和是：，第二个框框住的三个数的和是：，第三个框框住的三个数中的和是：；

(2)、这三个框框住的数的和分别能是81吗？若能，则分别求出最大的数a、b、c．

查看试题解析
20. 我们规定，若关于x的一元一次方程 $a x = b$ 的解为 $x = b - a$ ，则称该方程为“差解方程”．例如： $2 x = 4$ 的解为 $x = 2$ ，且 $2 = 4 - 2$ ，则该方程 $2 x = 4$ 是差解方程．

(1)、判断：方程 $3 x = 4.5$ 差解方程（填“是”或“不是”）

(2)、若关于x的一元一次方程 $4 x = m + 3$ 是差解方程，求m的值．

查看试题解析
21. 以直线 $A B$ 上一点O为端点作射线 $O C$ ，使 $∠ B O C = 60 °$ ，将一块直角三角板的直角顶点放在 $O$ 处，一边 $O D$ 放在射线 $O B$ 上，将直角三角板 $E O D$ 绕点O逆时针方向旋转直至 $O E$ 边第一次重合在射线 $O A$ 上停止．

(1)、如图1，边 $O D$ 在射线 $O B$ 上，则 $∠ C O E =$ ；

(2)、如图2，若 $O E$ 恰好平分 $∠ A O C$ ，则 $∠ D O B =$ ；

(3)、如图3，若 $∠ E O C = 105 °$ ，则 $∠ D O B =$ ；

(4)、在旋转过程中， $∠ E O C$ 与 $∠ D O B$ 始终保持的数量关系是，并请说明理由．

查看试题解析
22. 春节期间，七（1）班的李平、王丽等同学随家长一同到某公园游玩，下面是购买门票时，李平与他爸爸的对话（如图），试根据图中的信息，解答下列问题：

(1)、李平他们一共去了几个成人，几个学生？

(2)、请你帮助算一算，用哪种方式购票更省钱？说明理由．

(3)、购完票后，李平发现七⑵班的张明等8名同学和他们的12名家长共20人也来购票，请你为他们设计出最省的购票方案，并求出此时的购票费用.

查看试题解析
23. 阅读理解：
（探究与发现）

如图1，在数轴上点E表示的数是8，点F表示的数是4，求线段 $E F$ 的中点M所示的数对于求中点表示数的问题，只要用点E所表示的数-8，加上点F所表示的数4，得到的结果再除以2，就可以得到中点M所表示的数：即M点表示的数为： $\frac{- 8 + 4}{2} = - 2$ ．

(1)、（理解与应用）
把一条数轴在数m处对折，使表示-20和2020两数的点恰好互相重合，则 $m =$ ．

(2)、（拓展与延伸）
如图2，已知数轴上有A、B、C三点，点A表示的数是-6，点B表示的数是8． $A C = 18$ ．

若点A以每秒3个单位的速度向右运动，点C同时以每秒1个单位的速度向左运动设运动时间为t秒．

①点A运动t秒后，它在数轴上表示的数表示为（用含t的代数式表示）

②当点B为线段 $A C$ 的中点时，求t的值．

(3)、若（1）中点A、点C的运动速度、运动方向不变，点P从原点以每秒2个单位的速度向右运动，假设A、C、P三点同时运动，求多长时间点P到点 $A C$ 的距离相等?

查看试题解析